
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{2}}{2}$,1) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | x2+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{2}$+y2=1 | D. | x2+$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示
某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
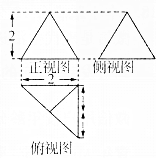 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2.
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?∈R,均有x2+sinx+1≥0 | B. | ?x∈R,使得x2+sinx+1<0 | ||
| C. | ?x∈R,使得x2+sinx+1≥0 | D. | ?x∈R,均有x2+sinx+1>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com