
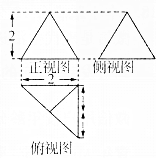
 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2.
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2. 分析 由已知可得:该几何体是一个以俯视图为底面的三棱锥,代入棱锥体积公式,可得棱锥的体积;计算出棱锥外接球的半径,代入球的表面积公式,可得球的表面积.
解答 解:由已知可得:
该几何体是一个以俯视图为底面的三棱锥,
其体积V=$\frac{1}{3}$×$\frac{1}{2}$×2×2×2=$\frac{4}{3}$,
设其外接球半径为R,
则(R-2)2+($\sqrt{2}$)2=R2,
解得:R=$\frac{3}{2}$,
故此三棱锥的外接球表面积S=4πR2=9π,
故答案为:$\frac{4}{3}$,9π
点评 本题考查的知识点是棱锥的体积和表面积,球的体积和和表面积,根据已知分析出几何体的形状,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | a(1+n%)13 | B. | a(1+n%)12 | C. | a(1+n%)11 | D. | $\frac{10}{9}a{(1-n%)^{12}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,6) | B. | (-1,0) | C. | (1,2) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
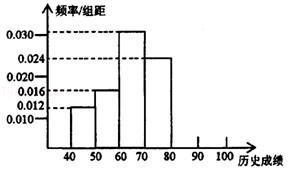 某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.
某校高一学生共有500人,为了了解学生的历史学习情况,随机抽取了50名学生,对他们一年来4次考试的历史平均成绩进行统计,得到频率分布直方图如图所示,后三组频数成等比数列.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com