
分析 (Ⅰ)函数f(x)=x2+bx-1的图象是开口朝上,且以直线x=-$\frac{b}{2}$为对称轴的抛物线,若函数y=f(x)在[1,+∞)上单调,则-$\frac{b}{2}$≤1,解处b的取值范围;
(Ⅱ)若函数y=|f(x)|-2有四个零点,则$1+\frac{{b}^{2}}{4}<2$,解得b的取值范围;
(Ⅲ)若函数y=|f(x)|在[0,|b|)上的最大值为g(b),结合二次函数的图象和性质分类讨论,可得答案.
解答 解:(Ⅰ)∵函数f(x)=x2+bx-1的图象是开口朝上,且以直线x=-$\frac{b}{2}$为对称轴的抛物线,…(2分)
∵y=f(x)在[1,+∞)上单调,
∴-$\frac{b}{2}$≤1,
即:b≥-2….(5分)
(Ⅱ)函数y=|f(x)|-2有四个零点,即函数y=|f(x)|与直线y=2有四个交点,
∵$f(x)={x^2}+bx-1={(x+\frac{b}{2})^2}-1-\frac{b^2}{4}$的最小值为$-1-\frac{{b}^{2}}{4}$
∴只需$1+\frac{{b}^{2}}{4}<2$ 即:b∈(-1,1)….(10分)
(Ⅲ)①当b>0时,函数y=|f(x)|在[0,b)上单调增,
g(b)=max{|f(0)|,|f(b)|}=max{1,|2b2-1|}=$\left\{\begin{array}{l}1,0<b<1\\ 2{b}^{2}-1,b≥1\end{array}\right.$…(12分)
②当b<0时,|f(0)|=f(|b|)=1,$f(-\frac{b}{2})=-1-\frac{b^2}{4}$
又$\left|f(-\frac{b}{2})\right|=1+\frac{{b}^{2}}{4}$>1,所以g(b)=$1+\frac{{b}^{2}}{4}$…(14分)
综上所述,g(b)=$\left\{\begin{array}{l}2{b}^{2}-1,b≥1\\ 1,0<b<1\\ 1+\frac{{b}^{2}}{4},b<0\end{array}\right.$;…(15分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示
某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示查看答案和解析>>
科目:高中数学 来源: 题型:填空题
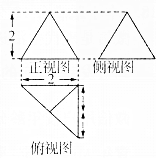 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2.
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,正视图和侧视图是全等的等腰三角形则此三棱锥的体积为:$\frac{4}{3}$cm3,此三棱锥的外接球表面积为:9πcm2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?∈R,均有x2+sinx+1≥0 | B. | ?x∈R,使得x2+sinx+1<0 | ||
| C. | ?x∈R,使得x2+sinx+1≥0 | D. | ?x∈R,均有x2+sinx+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com