
分析 解析式中分母含有未知数x,分母不能为0,可得定义域,利用分离常数法求解值域.
解答 解:由题意:分母不能为0,即x-2≠0,
解得:x≠2,
∴函数的定义域为(-∞,2)∪(2,+∞);
函数f(x)=$\frac{3x+1}{x-2}$化简可得:f(x)=$\frac{3(x-2)+7}{x-2}$=3+$\frac{7}{x-2}$
∵$\frac{7}{x-2}$≠0
∴f(x)≠3
∴函数的值域为(-∞,3)∪(3,+∞).
故答案为:(-∞,2)∪(2,+∞);(-∞,3)∪(3,+∞).
点评 本题考查了函数的定义域和值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


科目:高中数学 来源: 题型:选择题
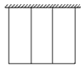 有一批材料可以建成200m的围墙,如果用此材料一遍靠墙围成一个矩形场地,中间用同样材料隔成三个面积相等的矩形,如图所示,则围成矩形场地最大面积为( )
有一批材料可以建成200m的围墙,如果用此材料一遍靠墙围成一个矩形场地,中间用同样材料隔成三个面积相等的矩形,如图所示,则围成矩形场地最大面积为( )| A. | 2000m2 | B. | 2500m2 | C. | 2800m2 | D. | 3000m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{2}$ | B. | 6 | C. | $\frac{7}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com