练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
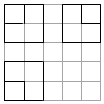
    9．如图，正方形网格中，粗实线画出的是某几何体的三视图，若该几何体的体积为7，则该几何体的表面积为（　　）
    A．18B．21C．24D．27

    分析 由三视图可知：该几何体为一个棱长为2x的正方体，在一个角去掉一个棱长为x的正方体余下的几何体．由该几何体的体积7=（2x）3-x3，解得x．即可得出表面积．

    解答 解：由三视图可知：该几何体为一个棱长为2x的正方体
    在一个角去掉一个棱长为x的正方体，余下的几何体．
    ∴该几何体的体积7=（2x）3-x3，解得x=1．
    ∴该几何体的表面积=6×22=24．
    故选：C．

    点评 本题考查了正方体的三视图、面积和体积计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知P为抛物线y2=4x上一个动点，Q为圆x2+（y-4）2=1上一个动点，当点P到点Q的距离与点P到抛物线的准线距离之和最小时，P点的横坐标为（　　）
    A．$\frac{\sqrt{17}}{8}$B．$\frac{9-\sqrt{17}}{8}$C．$\frac{9}{8}$D．$\sqrt{17}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知定义域为R的函数f（x）=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$是奇函数．
    （Ⅰ）求a，b的值；
    （Ⅱ）已知f（x）在定义域上为减函数，若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0（k为常数）恒成立．求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．数列{an}为正项等比数列，a1=2，$\frac{3}{8}$a4是a2和a3的等差中项，Sn为数列{bn}前n项和，2b2=b1+b3，$\sqrt{{S}_{n}}$是公差为1的等差数列．
    （1）求数列{nan}的前n项和Tn；
    （2）求数列{bn}通项公式；
    （3）是否存在n∈N*，使Sn=an成立？若存在，求出所有n的值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=xlnx+ax2-x+a（a∈R）在其定义域内有两个不同的极值点．
    （1）求a的取值范围．
    （2）设f（x）的两个极值点为x1，x2，证明x1x2＞e2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）是定义在R上的减函数，其导函数f'（x）满足$\frac{f（x）+xf'（x）}{f'（x）}＜1$，则下列结论中正确的是（　　）
    A．f（x）＞0恒成立B．f（x）＜0
    C．当且仅当x∈（-∞，1），f（x）＜0D．当且仅当x∈（1，+∞），f（x）＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．某中学有篮球社，吉他社，传统文化社，动漫社等多个社团，其中传统文化社借端午节来临之际举行包粽子送祝福活动，随机调查了高三50名男女生对粽子口味的喜好，统计如下表：
      甜味粽 咸味粽 南国风味
     枣子粽豆沙粽  玫瑰粽 蛋黄粽 猪肉粽 什锦粽
     男生 4 3 1 10 4 3
     女生6  5 5 5 13
    （1）按以上统计数据填写下面的2×2列联表，并运用独立性检验思想，判断是否有97.5%把握认为甜味粽和咸味粽的喜好与性别有关系？
      甜味粽咸味粽  合计
     男生   
     女生   
     合计   
    参考公式及临界值表如下：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    （2）从被调查的50人中对玫瑰粽和什锦粽喜好的同学按照分层抽样的方法抽取4名同学按顺序进行深度调查，则前两位接受调查的都是喜好玫瑰粽同学的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．定义在R上的奇函数f（x）满足f（2-x）=f（x），当x∈[0，1]时，f（x）=$\sqrt{x}$．又函数g（x）=cos$\frac{πx}{2}$，x∈[-3，3]，则函数F（x）=f（x）-g（x）的所有零点之和等于（　　）
    A．-$\frac{3}{2}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{3}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若直线2ax-by+2=0（a，b∈R）始终平分圆x2+y2+2x-4y+1=0的周长，则ab的最大值是$\frac{1}{4}$．

    查看答案和解析>>

    同步练习册答案