Question

4．已知函数f（x）=xlnx+ax²-x+a（a∈R）在其定义域内有两个不同的极值点．
（1）求a的取值范围．
（2）设f（x）的两个极值点为x₁，x₂，证明x₁x₂＞e²．

Answer 1

分析 （1）由导数与极值的关系知可转化为方程f′（x）=lnx-ax=0在（0，+∞）有两个不同根；再转化为函数y=lnx与函数y=ax的图象在（0，+∞）上有两个不同交点，或转化为函数g（x）=$\frac{lnx}{x}$与函数y=-2a的图象在（0，+∞）上有两个不同交点； 从而求解；
（2）要证明x₁x₂＞e²．只需证明lnx₁+lnx₂＞2
?-2a（x₁+x₂）＞2，?$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$（x₁+x₂）＞2，即只需证明$ln\frac{{x}_{1}}{{x}_{2}}＞\frac{2（{x}_{1}-{x}_{2}）}{{x}_{1}+{x}_{2}}$，
令$\frac{{x}_{1}}{{x}_{2}}=t$，则t＞1，只需证明$lnt＞\frac{2（t-1）}{t+1}$，
设g（t）=lnt-$\frac{2（t-1）}{t+1}$  （t＞1），根据函数的单调性证出结论即可

解答 解：（1）函数f（x）=xlnx+ax²-x+a（a∈R）的定义域为（0，+∞），f′（x）=lnx+2ax．
∵函数f（x）=xlnx+ax²-x+a（a∈R）在其定义域内有两个不同的极值点．∴方程f′（x）=0在（0，+∞）有两个不同根；
转化为函数g（x）=$\frac{lnx}{x}$与函数y=-2a的图象在（0，+∞）上有两个不同交点．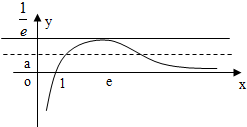
又g′（x）=$\frac{1-lnx}{{x}^{2}}$，即0＜x＜e时，g′（x）＞0，x＞e时，g′（x）＜0，
故g（x）在（0，e）上单调增，在（e，+∞）上单调减．故g（x）_极大=g（e）=$\frac{1}{e}$．
又g（x）有且只有一个零点是1，且在x→0时，g（x）→-∞，在在x→+∞时，g（x）→0，
故g（x）的草图如右图，
∴0$＜-2a＜\frac{1}{e}$，即-$\frac{1}{2e}＜a＜0$．故a的取值范围为（-$\frac{1}{2e}，0$）．
（2）由（Ⅰ）可知x₁，x₂分别是方程lnx-ax=0的两个根，
      即lnx₁=-2ax₁，lnx₂=-2ax₂，
设x₁＞x₂，作差得$ln\frac{{x}_{1}}{{x}_{2}}=-2a（{x}_{1}-{x}_{2}）$．得-2a=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$．
要证明x₁x₂＞e²．只需证明lnx₁+lnx₂＞2
?-2a（x₁+x₂）＞2，?$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$（x₁+x₂）＞2，即只需证明$ln\frac{{x}_{1}}{{x}_{2}}＞\frac{2（{x}_{1}-{x}_{2}）}{{x}_{1}+{x}_{2}}$，
令$\frac{{x}_{1}}{{x}_{2}}=t$，则t＞1，只需证明$lnt＞\frac{2（t-1）}{t+1}$，
设g（t）=lnt-$\frac{2（t-1）}{t+1}$  （t＞1），$g′（t）=\frac{（t-1）^{2}}{t（t+1）}＞0$．
∴函数g（t）在（1，+∞）上单调递增，
∴g（t）＞g（1）=0，故$lnt＞\frac{2（t-1）}{t+1}$成立．
∴x₁x₂＞e²成立．

点评 题考查了导数的综合应用及分类讨论，转化思想，数形结合的思想方法的应用，属于难题．