
【题目】已知动圆![]() 过点
过点![]() ,且与圆
,且与圆![]() 相内切.
相内切.
(I)求动圆![]() 的圆心的轨迹方程;
的圆心的轨迹方程;
(II)设直线![]() (其中
(其中![]() 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点![]() ,D,与双曲线
,D,与双曲线![]() 交于不同两点
交于不同两点![]() ,问是否存在直线
,问是否存在直线![]() ,使得向量
,使得向量![]() ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
【答案】(Ⅰ) ![]() (Ⅱ) 满足条件的直线共有9条.
(Ⅱ) 满足条件的直线共有9条.
【解析】试题分析:(I)由|AM|=4<R得点A(-2,0)在圆M内,设动圆C的半径为r,依题意得r=|CA|,且|CM|=R-r,|CM+|CA|=8>|AM|,由定义得圆心C的轨迹是中心在原点,以A,M两点为焦点,长轴长为8的椭圆,再根据a,b,c的关系解答即可.
(II)直线l: ![]() 与
与![]() 联立得
联立得![]() ,同理得
,同理得![]() ,又因为
,又因为![]() ,所以
,所以![]() ,即
,即![]() ,又其中k,m∈Z即可求出k,m的数值.
,又其中k,m∈Z即可求出k,m的数值.
试题解析:
(1)圆![]() , 圆心
, 圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() .
.
∵![]() ,∴点
,∴点![]() 在圆
在圆![]() 内.
内.
设动圆![]() 的半径为
的半径为![]() ,圆心为
,圆心为![]() ,依题意得
,依题意得![]() ,且
,且![]() ,
,
即![]() .
.
∴圆心![]() 的轨迹是中心在原点,以
的轨迹是中心在原点,以![]() 两点为焦点,长轴长为
两点为焦点,长轴长为![]() 的椭圆,
的椭圆,
设其方程为![]() , 则
, 则![]() .∴
.∴![]() .
.
∴所求动圆![]() 的圆心的轨迹方程为
的圆心的轨迹方程为![]() .
.
(2)由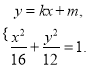 消去
消去![]() 化简整理得:
化简整理得: ![]() .
.
设![]() ,
, ![]() ,则
,则![]() .
.
![]()
![]() . ①
. ①
由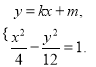 消去
消去![]() 化简整理得:
化简整理得: ![]() .
.
设![]() ,则
,则![]() ,
,
![]()
![]() . ②
. ②
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() .∴
.∴![]() 或
或![]() .解得
.解得![]() 或
或![]() .
.
当![]() 时,由①、②得
时,由①、②得 ![]()
∵![]() Z,∴
Z,∴![]() 的值为
的值为![]()
![]() ,
, ![]() ,
, ![]()
![]() ;
;
当![]() ,由①、②得
,由①、②得 ![]() ,
,
∵![]() Z,∴
Z,∴![]() .
.
∴满足条件的直线共有9条.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 是正三角形,
是正三角形, ![]() 平面
平面![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上,且
上,且![]() .
.
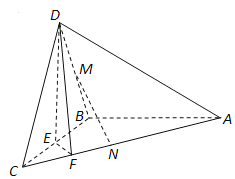
(1)求三棱锥![]() 的体积;
的体积;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() 为
为![]() 中点,
中点, ![]() 在棱
在棱![]() 上,且
上,且![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,下列说法正确的是____ (填序号).
(1)直线AC1在平面CC1B1B内.
(2)设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1.
(3)由A、C1、B1确定的平面是ADC1B1.
(4)由A、C1、B1确定的平面与由A、C1、D确定的平面是同一个平面.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() .
.
(1)若数列![]() 是首项为正数,公比为
是首项为正数,公比为![]() 的等比数列.
的等比数列.
①求证:数列![]() 为等比数列;
为等比数列;
②若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)已知![]() 为递增数列,即
为递增数列,即![]() .若对任意
.若对任意![]() ,数列
,数列![]() 中都存在一项
中都存在一项![]() 使得
使得![]() ,求证:数列
,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 。
。
(Ⅰ)求证:直线![]() 与圆C恒有两个交点;
与圆C恒有两个交点;
(Ⅱ)求出直线![]() 被圆C截得的最短弦长,并求出截得最短弦长时的
被圆C截得的最短弦长,并求出截得最短弦长时的![]() 的值;
的值;
(Ⅲ)设直线![]() 与圆C的两个交点为M,N,且
与圆C的两个交点为M,N,且![]() (点C为圆C的圆心),求直线
(点C为圆C的圆心),求直线![]() 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com