某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如下：
| API |
[0，50] |
（50，100] |
（100，150] |
（150，200] |
（200，250] |
（250，300] |
＞300 |
| 空气质量 |
优 |
良 |
轻微污染 |
轻度污染 |
中度污染 |
中度重污染 |
重度污染 |
| 天数 |
4 |
13 |
18 |
30 |
9 |
11 |
15 |
记某企业每天由空气污染造成的经济损失S（单位：元），空气质量指数API为ω．在区间[0，100]对企业没有造成经济损失；在区间（100，300]对企业造成经济损失成直线模型（当API为150时造成的 经济损失为500元，当API为200时，造成的经济损失为700元）；当API大于300时造成的 经济损失为2000元；
（1）试写出是S（ω）的表达式：
（2）试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？
附：
| P（K2≥k0） |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k0 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
K
2=
| m(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
|
非重度污染 |
重度污染 |
合计 |
| 供暖季 |
|
|
|
| 非供暖季 |
|
|
|
| 合计 |
|
|
100 |
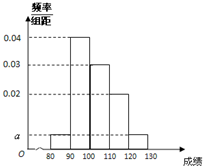为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]
如图所示的圆盘由八个全等的扇形构成，指针绕中心旋转，可能随机停止则指针停止在阴影部分内的概率是（ ）