
| A. | 0 | B. | 1 | C. | e | D. | 2e |
分析 根据函数的单调性的定义可得g(x)在(-∞,0]内单调递增,根据题意作出函数f(x)的简图,利用树形结合的思想即可求出.
解答 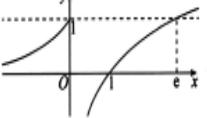 解:对?x1,x2∈(-∞,0],且x1≠x2均有x1g(x1)+x2g(x2)>x1g(x2)+x2g(x1),
解:对?x1,x2∈(-∞,0],且x1≠x2均有x1g(x1)+x2g(x2)>x1g(x2)+x2g(x1),
∴[g(x2)-g(x1)](x2-x1)>0,
∴g(x)在(-∞,0]内单调递增,
根据题意作出函数f(x)的简图,如图所述,
令f(x)≤1,由f(x)的图象可知x≤e,
若f(x-a)≤1,则x≤e+a,
∴D=(-∞,e+a],
又2e∈D,
∴2e≤a+e,
∴a≥e,则a的最小值是e,
故选:C.
点评 本题考查了函数的单调性和函数的单调性的应用,考查了转化思想和数形结合的思想,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
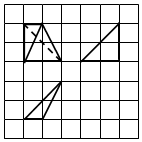 如图,网格的小正方形的边长是1,在其上用粗实线和粗虚线画出了某多面体的三视图,则这个多面体的体积是( )
如图,网格的小正方形的边长是1,在其上用粗实线和粗虚线画出了某多面体的三视图,则这个多面体的体积是( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 7 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 种植地编号 | A1 | A2 | A3 | A4 | A5 |
| (x,y,z) | (0,1,0) | (1,2,1) | (2,1,1) | (2,2,2) | (0,1,1) |
| 种植地编号 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (2,1,2) | (2,0,1) | (2,2,1) | (0,2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
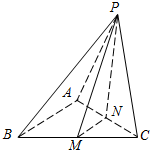 如图,在三棱锥P-ABC中,PA=PC,BC=4,AC=2.M为BC的中点,N为AC上一点,且MN∥平面PAB,MN=$\sqrt{3}$.求证:
如图,在三棱锥P-ABC中,PA=PC,BC=4,AC=2.M为BC的中点,N为AC上一点,且MN∥平面PAB,MN=$\sqrt{3}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | 4 | C. | $\frac{40}{9}$ | D. | $\frac{56}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com