Question

1．设AB是椭圆$\frac{x^2}{16}+\frac{y^2}{4}=1$的长轴，若把AB分成10等分，依次过每个分点作AB的垂线，交椭圆的上半部分于P₁、P₂、…P₉．F₁为椭圆的左焦点，则|F₁A|+|F₁P₁|+|F₁P₂|+…+|F₁P₉|+|F₁B|的值44．

Answer 1

分析 由题意可知当i+j=10时有：|P_iF₁|=|P_jF₂|，其中i、j∈{1，2，3，…，9}，由椭圆定义可知：|P_iF₁|+|P_iF₂|=2a=2×4=8，i∈{1，2，3，…，9}，根据椭圆性质则|F₁P₁|+|F₁P₂|+…+|F₁P₉|=36，|F₁A|+|F₁B|=2a=8，即可求得答案．

解答 解：F是椭圆的一个焦点，不妨令F为左焦点F₁，则右焦点为F₂，
分别连结点F₂与P₁，P₂，…P₉九个点，
易知当i+j=10时有：|P_iF₁|=|P_jF₂|，其中i、j∈{1，2，3，…，9}，
由椭圆定义可知：|P_iF₁|+|P_iF₂|=2a=2×4=8，i∈{1，2，3，…，9}，
∴2（|F₁P₁|+|F₁P₂|+…+|F₁P₉|）=9×8=72，
即|F₁P₁|+|F₁P₂|+…+|F₁P₉|=36，
则|F₁A|+|F₁B|=2a=8，
∴|F₁A|+|F₁P₁|+|F₁P₂|+…+|F₁P₉|+|F₁B|=36+8=44，
故答案为：44．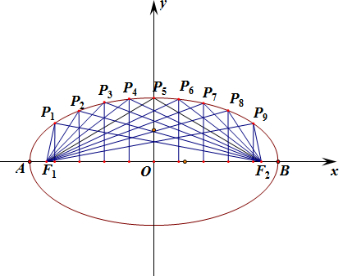

点评 本题考查椭圆的定义，考查椭圆方程的应用，考查计算能力，属于中档题．