
【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn= ![]() (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
【答案】
(1)解:由题意,得Sn+1=tSn+1,令n=1有,S2=tS1+1,
∴a1+a2=ta1+1.代入a1=1,a2=2有t=2.
∴Sn+1=2Sn+1,则Sn=2Sn﹣1+1(n≥2).
两式相减有,an+1=2an,即 ![]() ,且
,且 ![]() 符合.
符合.
∴{an}为公比为2的等比数列.
则 ![]() ,
, ![]()
(2)证明:bn= ![]() =
= ![]() <
< ![]() .
.
∴当n≥2时,
Tn=b1+b2+…+bn ![]() =
= 
【解析】(1)把点(Sn , Sn+1)代入直线y=tx+1,结合a1=1,a2=2求得t,可得数列递推式,进一步可得{an}为公比为2的等比数列.再由等比数列的通项公式和前n项和公式求得Sn及an;(2)把an代入bn= ![]() ,放缩可得
,放缩可得 ![]() (n≥2),代入Tn=b1+b2+…+bn , 由等比数列的前n项和证得当n≥2时,Tn<2.
(n≥2),代入Tn=b1+b2+…+bn , 由等比数列的前n项和证得当n≥2时,Tn<2.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系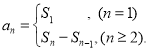 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某展览馆用同种规格的木条制作如图所示的展示框,其内框与外框均为矩形,并用木条相互连结,连结木条与所连框边均垂直.水平方向的连结木条长均为8cm,竖直方向的连结木条长均为4cm,内框矩形的面积为3200cm2 . (不计木料的粗细与接头处损耗) 
(1)如何设计外框的长与宽,才能使外框矩形面积最小?
(2)如何设计外框的长与宽,才能使制作整个展示框所用木条最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: ![]() =3n2an+
=3n2an+![]() ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三内角A,B,C所对的边分别是a,b,c,△ABC的面积S= ![]() 且sinA=
且sinA= ![]() .
.
(1)求sinB;
(2)若边c=5,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(2)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的是( )
A.已知f(x)=sin2x+ ![]() ,则f(x)的最小值是2
,则f(x)的最小值是2 ![]()
B.已知数列{an}的通项公式为an=n+ ![]() ,则{an}的最小项为2
,则{an}的最小项为2 ![]()
C.已知实数x,y满足x+y=2,则xy的最大值是1
D.已知实数x,y满足xy=1,则x+y的最小值是2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知数列![]() (
(![]() ,
, ![]() )满足
)满足![]() ,
,  其中
其中![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的取值范围;
的取值范围;
(2)设集合![]() .
.
①若![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
②是否存在实数![]() ,
, ![]() ,使
,使![]() ,
, ![]() ,
, ![]() 都属于
都属于![]() ?若存在,请求出实数
?若存在,请求出实数![]() ,
, ![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com