
【题目】已知△ABC的三内角A,B,C所对的边分别是a,b,c,△ABC的面积S= ![]() 且sinA=
且sinA= ![]() .
.
(1)求sinB;
(2)若边c=5,求△ABC的面积S.
【答案】
(1)解:由余弦定理有c2=a2+b2﹣2abcosC,∴a2+b2﹣c2=2abcosC,
则 ![]() ,又
,又 ![]() ,
,
∴cosC=sinC,tanC=1,在△ABC中 ![]() ,
,
∵ ![]() ,在△ABC中
,在△ABC中 ![]() 或
或 ![]() ,但A+B+C=π,
,但A+B+C=π,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
sinB= ![]() =
= ![]() ×
× ![]() =
= ![]()
(2)解:由正弦定理有 ![]() ,又c=5,∴
,又c=5,∴ ![]() ,得b=7,
,得b=7,
∴S= ![]() bcsinA=
bcsinA= ![]() =
= ![]()
【解析】(1)利用余弦定理、三角形面积计算公式可得C,再利用同角三角函数基本关系式、三角形内角和定理、和差公式即可得出.(2)利用正弦定理、三角形面积计算公式即可得出.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,sin2B=2sinAsinC.
(1)若a=b,求cosB的值;
(2)若B=60°,△ABC的面积为4 ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=﹣f(x),当﹣1≤x<1时,f(x)=x3 , 若函数g(x)=f(x)﹣loga|x|至少6个零点,则a取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=![]() ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn= ![]() (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报说,未来三天每天下雨的概率都是0.6,用1、2、3、4表示不下雨,用5、6、7、8、9、0表示下雨,利用计算机生成下列20组随机数,则未来三天恰有两天下雨的概率大约是 .
757 220 582 092 103 000 181 249 414 993
010 732 680 596 761 835 463 521 186 289.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
B.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ
D.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如图部分频率分布直方图.观察图形的信息,回答下列问题. 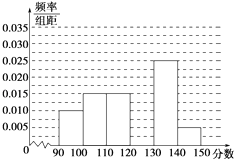
(1)从该校高三模拟考试的成绩中随机抽取一份,利用随机事件频率估计概率,求数学分数恰在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com