
如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点, ,
,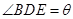 ,
,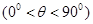 .
.
(1)当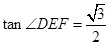 时,求
时,求 的大小;
的大小;
(2)求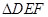 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时 的值.
的值.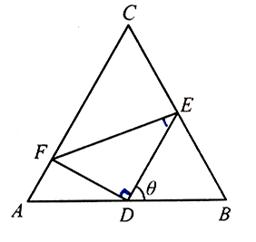
(1)θ=60°;(2)当θ=45°时,S取最小值 .
.
解析试题分析:本题主要考查正弦定理、直角三角形中正切的定义、两角和的正弦公式、倍角公式、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,在 中,
中, ,①,而在
,①,而在 中,利用正弦定理,用
中,利用正弦定理,用 表示DE,在
表示DE,在 中,利用正弦定理,用
中,利用正弦定理,用 表示DF,代入到①式中,再利用两角和的正弦公式展开,解出
表示DF,代入到①式中,再利用两角和的正弦公式展开,解出 ,利用特殊角的三角函数值求角
,利用特殊角的三角函数值求角 ;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.
;第二问,将第一问得到的DF和DE代入到三角形面积公式中,利用两角和的正弦公式和倍角公式化简表达式,利用正弦函数的有界性确定S的最小值.
在△BDE中,由正弦定理得 ,
,
在△ADF中,由正弦定理得 . 4分
. 4分
由tan∠DEF= ,得
,得 ,整理得
,整理得 ,
,
所以θ=60°. 6分
(2)S=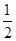 DE·DF=
DE·DF=
 . 10分
. 10分
当θ=45°时,S取最小值 . 12分
. 12分
考点:正弦定理、直角三角形中正切的定义、两角和的正弦公式、倍角公式、三角形面积公式.


科目:高中数学 来源: 题型:解答题
如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.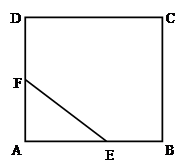
(1)求总费用y关于θ的函数.
(2)求最小的总费用和对应θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•重庆)设函数f(x)=sinxcosx﹣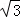 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函数y=f(x)的图象按 =(
=( ,
,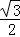 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙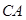 、
、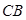 的夹角为
的夹角为 (即
(即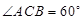 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料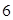 米(两面墙的长均大于
米(两面墙的长均大于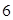 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记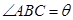 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 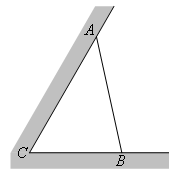
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com