
(13分)(2011•重庆)设函数f(x)=sinxcosx﹣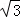 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函数y=f(x)的图象按 =(
=( ,
,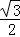 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
(I)π(II)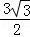
解析试题分析:(I)先利用诱导公式,二倍角公式与和角公式将函数解析式化简整理,然后利用周期公式可求得函数的最小正周期.
(II)由(I)得函数y=f(x),利用函数图象的变换可得函数y=g(x)的解析式,通过探讨角的范围,即可的函数g(x)的最大值.
解:(I)∵f(x)=sinxcosx﹣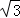 cos(x+π)cosx
cos(x+π)cosx
=sinxcosx+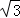 cosxcosx
cosxcosx
=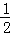 sin2x+
sin2x+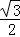 cos2x+
cos2x+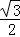
=sin(2x+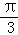 )+
)+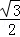
∴f(x)的最小正周期T=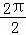 =π
=π
(II)∵函数y=f(x)的图象按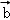 =(
=(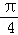 ,
,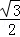 )平移后得到的函数y=g(x)的图象,
)平移后得到的函数y=g(x)的图象,
∴g(x)=sin(2x+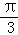 ﹣
﹣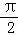 )+
)+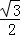 +
+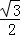 =sin(2x﹣
=sin(2x﹣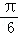 )+
)+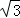
∵0<x≤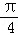 ∴
∴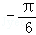 <2x﹣
<2x﹣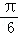 ≤
≤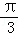 ,
,
∴y=g(x)在(0,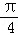 ]上的最大值为:
]上的最大值为: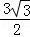 .
.
点评:本题考查了三角函数的周期及其求法,函数图象的变换及三角函数的最值,各公式的熟练应用是解决问题的根本,体现了整体意识,是个中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将 的图象向左平移
的图象向左平移 (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的图象上各最高点到点
的图象上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点, ,
,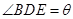 ,
,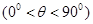 .
.
(1)当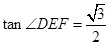 时,求
时,求 的大小;
的大小;
(2)求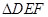 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时 的值.
的值.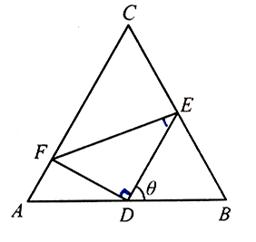
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com