
已知函数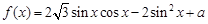 ,
,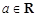 .
.
(1)求函数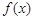 的最小正周期;
的最小正周期;
(2)若函数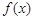 有零点,求实数
有零点,求实数 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
(13分)(2011•重庆)设函数f(x)=sinxcosx﹣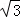 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函数y=f(x)的图象按 =(
=( ,
,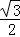 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
电流强度I与时间t的关系式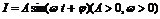 。(1)在一个周期内
。(1)在一个周期内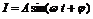 如图所示,试根据图象写出
如图所示,试根据图象写出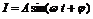 的解析式;(2)为了使
的解析式;(2)为了使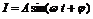 中t在任意一段
中t在任意一段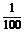 秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数
秒的时内I能同时取最大值|A|和最小值-|A|,那么正整数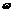 的最小值为多少?
的最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com