
(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将 的图象向左平移
的图象向左平移 (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的图象上各最高点到点
的图象上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的单调增区间.
的单调增区间.
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
已知函数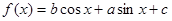 .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)当 ,
, 时,函数
时,函数 的图象关于
的图象关于 对称,求函数
对称,求函数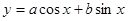 的对称轴;
的对称轴;
(3)若 图象上有一个最低点
图象上有一个最低点 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得 的图象,又知
的图象,又知 的所有正根从小到大依次为
的所有正根从小到大依次为 ,
, ,…
,… ,…且
,…且 ,求
,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.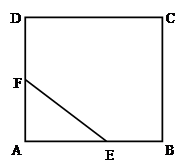
(1)求总费用y关于θ的函数.
(2)求最小的总费用和对应θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某实验室一天的温度(单位: )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•重庆)设函数f(x)=sinxcosx﹣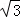 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R)
(I)求f(x)的最小正周期;
(II)若函数y=f(x)的图象按 =(
=( ,
,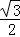 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0, ]上的最大值.
]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com