
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
(1) ϕ=? (2) 单调区间为[kπ+
(2) 单调区间为[kπ+ ,kπ+
,kπ+ ],k∈Z ; (3)见解析.
],k∈Z ; (3)见解析.
解析试题分析:(1)函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .可得到
.可得到 +ϕ=kπ+
+ϕ=kπ+ ,k∈Z.由此方程求出φ值,
,k∈Z.由此方程求出φ值,
(2)求函数y=f(x)的单调增区间可令2kπ? ≤2x?
≤2x? ≤2kπ+
≤2kπ+ ,k∈Z,解出x的取值范围即可得到函数的单调递增区间.
,k∈Z,解出x的取值范围即可得到函数的单调递增区间.
(3)由五点法作图的规则,列出表格,作出图象.
试题解析:(1)因为x= 是函数y=f(x)的图象的对称轴,
是函数y=f(x)的图象的对称轴,
所以sin(2× +ϕ)=±1,即
+ϕ)=±1,即 +ϕ=kπ+
+ϕ=kπ+ ,k∈Z .2分
,k∈Z .2分
因为-π<φ<0,所以ϕ=? .2分
.2分
(2)由(1)知ϕ=? ,因此y=sin(2x?
,因此y=sin(2x? ).
).
由题意得2kπ? ≤2x?
≤2x? ≤2kπ+
≤2kπ+ ,k∈Z, 2分
,k∈Z, 2分
所以函数y=sin(2x? )的单调增区间为[kπ+
)的单调增区间为[kπ+ ,kπ+
,kπ+ ],k∈Z 2分
],k∈Z 2分
(3)由y=sin(2x? )知: ..2分
)知: ..2分x 0 


π .y 
-1 0 1 0 
故函数y=f(x)在区间[0,π]上的图象是 2分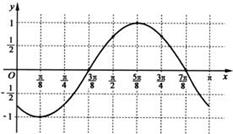


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
已知函数
(1)求函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若将函数的图像向右平移 个单位,得到函数
个单位,得到函数 的图像,求
的图像,求 在区间
在区间 上的最大值和最小值,并求出相应的x的取值。
上的最大值和最小值,并求出相应的x的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
先解答(1),再通过结构类比解答(2):
(1)请用tanx表示 ,并写出函数
,并写出函数 的最小正周期;
的最小正周期;
(2)设 为非零常数,且
为非零常数,且 ,试问
,试问 是周期函数吗?证明你的结论.
是周期函数吗?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将 的图象向左平移
的图象向左平移 (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的图象上各最高点到点
的图象上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的单调增区间.
的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com