
如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米,设角AEF=θ,θ ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.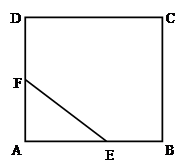
(1)求总费用y关于θ的函数.
(2)求最小的总费用和对应θ的值.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
某同学用“五点法”画函数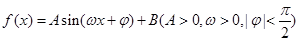 在某一
在某一
个周期内的图象时,列表并填入的部分数据如下表:
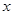 | 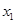 | 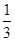 | 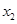 | 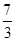 | 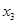 |
 |  | 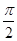 | 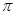 | 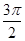 | 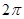 |
 |  | 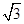 |  | 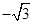 |  |
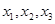 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式; 的图象沿
的图象沿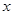 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数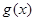 ,若函数
,若函数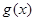 在
在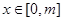 (其中
(其中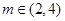 )上的值域为
)上的值域为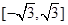 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求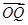 与
与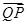 夹角
夹角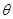 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将 的图象向左平移
的图象向左平移 (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的图象上各最高点到点
的图象上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
(1)求函数f(x)的解析式;
(2)若锐角θ满足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数 的一段图象过点(0,1),如图所示.(1)求函数
的一段图象过点(0,1),如图所示.(1)求函数 的表达式;(2)将函数
的表达式;(2)将函数 的图象向右平移
的图象向右平移 个单位,得函数
个单位,得函数 的图象,求
的图象,求 的最大值,并求出此时自变量x的集合.
的最大值,并求出此时自变量x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正三角形ABC的边长为2,D,E,F分别在三边AB,BC和CA上,且D为AB的中点, ,
,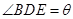 ,
,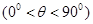 .
.
(1)当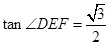 时,求
时,求 的大小;
的大小;
(2)求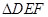 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时 的值.
的值.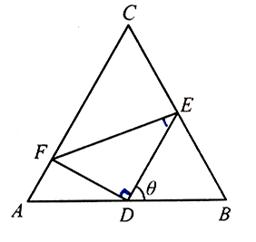
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com