练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数)．
    （1）求函数的最小正周期；
    （2）若，求的值．

    （1）;（2）

    解析试题分析：（1）先利用2倍角公式可求得，再利用两角和与差公式求得：即；（2）先将代入可得，又利用和与差公式拆开可得：然后利用题中条件求解的值，再带入即可求解.
    （1） ;
    （2） *，，,，可求得＝，代入*式可求得.
    考点：1三角函数和与差公式，2三角函数的性质.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数
    (1).求的周期和单调递增区间；
    (2).若关于x的方程在上有解，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数．
    (1)求函数的最小正周期；
    (2)求函数的递增区间；
    (3)当时，求的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，，且.
    （1）求的值；
    （2）若，，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图,有一块正方形区域ABCD,现在要划出一个直角三角形AEF区域进行绿化,满足:EF=1米，设角AEF=θ,θ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元．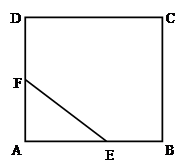

    (1)求总费用y关于θ的函数．
    (2)求最小的总费用和对应θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知a>0，函数f(x)＝－2asin(2x＋)＋2a＋b，当x∈[0，]时，－5≤f(x)≤1．
    (1)求常数a，b的值；
    (2)设g(x)＝f(x＋)且lg[g(x)]>0，求g(x)的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图，A，B是单位圆上的两个质点，点B坐标为(1,0)，∠BOA＝60°.质点A以1 rad/s的角速度按逆时针方向在单位圆上运动，质点B以1 rad/s的角速度按顺时针方向在单位圆上运动．

    (1)求经过1 s 后，∠BOA的弧度；
    (2)求质点A，B在单位圆上第一次相遇所用的时间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，.
    （1）求的值；
    （2）求的最大值和最小正周期；
    （3）若，是第二象限的角，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知．（1）求函数的值域；（2）求函数的最大值和最小值．

    查看答案和解析>>

    同步练习册答案