练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (本小题满分12分)已知函数++(为常数)
    (1)求函数的最小正周期；
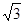    (2)若函数在上的最大值与最小值之和为，求实数的值．

    （1）；（2）．

    解析试题分析：（1）利用两角和与差的正弦公式以及辅助角公式对进行三角恒等变形，即可得到
    ，从而的最小正周期；（2）由（1）中求得的的表达式，可得当时，，从而可求得，，进一步可得．
    （1）∵ 
    ∴函数的最小正周期      6分；
    ∵，∴，
    ∴当，即时，，
    当，即时，，    
    由题意，有∴   12分．
    考点：1．三角恒等变形；2．三角函数的图像与性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知
    （1）求函数的值域；
    （2）求函数的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    扇形AOB的周长为8 cm.
    (1)若这个扇形的面积为3 cm2，求圆心角的大小；
    (2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数，x∈R(其中A＞0，ω＞0,)的周期为π，且图象上一个最低点为M.
    (1)求f(x)的解析式；
    (2)当x∈时，求f(x)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    若函数的图象与直线y＝m相切，相邻切点之间的距离为.
    (1)求m和a的值；
    (2)若点A(x0，y0)是y＝f(x)图象的对称中心，且，求点A的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    是否存在实数a，使得函数在闭区间上的最大值是1？若存在，求出对应的a值？若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （13分）（2011•重庆）设函数f（x）=sinxcosx﹣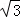cos（x+π）cosx，（x∈R）
    （I）求f（x）的最小正周期；
    （II）若函数y=f（x）的图象按=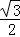（，）平移后得到的函数y=g（x）的图象，求y=g（x）在（0，]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    如图所示，某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料，已知已有两面墙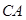、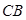的夹角为（即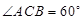），现有可供建造第三面围墙的材料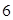米（两面墙的长均大于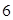米），为了使得仓库的面积尽可能大，记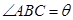，问当为多少时，所建造的三角形露天仓库的面积最大，并求出最大值？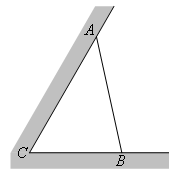

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知向量, 设函数.
    （1）求f (x)的最小正周期.
    （2）求f (x)在上的最大值和最小值.

    查看答案和解析>>

    同步练习册答案