
若函数 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且 ,求点A的坐标.
,求点A的坐标.
(1)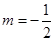 或
或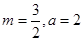 ;(2)
;(2)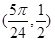 或
或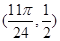 .
.
解析试题分析:(1)利用二倍角公式的降幂变形以及辅助角公式,可以把 变形为
变形为 ,又根据条件
,又根据条件 的图像与直线y=m相切,可知m为函数
的图像与直线y=m相切,可知m为函数 的最大值或最小值,即
的最大值或最小值,即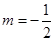 或
或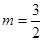 ,而相邻两个点之间的距离即相邻两条对称轴之间的距离即为函数的周期
,而相邻两个点之间的距离即相邻两条对称轴之间的距离即为函数的周期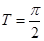 ,从而求得a=2;(2)根据正弦函数
,从而求得a=2;(2)根据正弦函数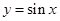 的对称中心为
的对称中心为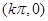 ,可令
,可令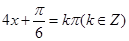 ,解得
,解得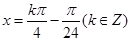 ,即
,即 ,又有
,又有 ,可求得整数k的值为1或2,从而可以得到对称中心的坐标为
,可求得整数k的值为1或2,从而可以得到对称中心的坐标为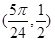 或
或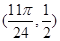 .
.
(1) ,
,
由题意 的图像与直线y=m相切,∴m为
的图像与直线y=m相切,∴m为 的最大值或最小值,即
的最大值或最小值,即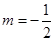 或
或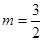 ;
;
又∵相邻两切点之间的距离为 ,∴函数
,∴函数 的周期为
的周期为 ,∴
,∴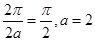 ;
;
(2)由(1)可知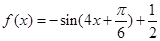 ,
,
令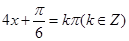 ,解得
,解得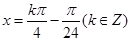 ,
,
即 ,又∵
,又∵ ,∴
,∴ ,解得
,解得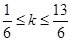 ,∵
,∵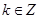 ,∴k=1或k=2,∴点A的坐标为
,∴k=1或k=2,∴点A的坐标为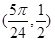 或
或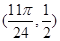 .
.
考点:1、三角恒等变形;2、三角函数的图像与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图所示,一个半圆和长方形组成的铁皮,长方形的边 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形 ,使得
,使得 ,
, .
.
(1)设 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正方形ABCD在直线MN的上方,边BC在直线MN上,E是线段BC上一点,以AE为边在直线MN的上方作正方形AEFG,其中AE=2,记∠FEN=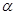 ,△EFC的面积为
,△EFC的面积为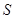 .
.
(1)求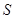 与
与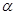 之间的函数关系;
之间的函数关系;
(2)当角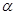 取何值时
取何值时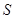 最大?并求
最大?并求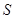 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com