练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    已知圆在极坐标方程为，直线的参数方程为（为参数）.若直

    线与圆相交于不同的两点.

    （Ⅰ）写出圆的直角坐标方程，并求圆心的坐标与半径；

    （Ⅱ）若弦长，求直线的斜率.

    【答案】（I）；（II）或．

    【解析】

    试题分析：（I）化极坐标方程为直角坐标方程主要是利用公式，，来完成．代入可得，配方得，所以圆心为，半径为；（II）在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题，通常将极坐标方程与参数方程均化为直角坐标方程来解决. 由直线的参数方程知直线过定点，直线的方程为.利用弦长等于可求得斜率或.

    试题解析：（I）由，得.

    将，代入可得，

    配方，得，所以圆心为，半径为.

    （II）由直线的参数方程知直线过定点，

    则由题意，知直线的斜率一定存在，因此不妨设直线的方程为的方程为.

    因为,所以，解得或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司生产一种产品，每年需投入固定成本25万元，此外每生产1件这样的产品，还需增加投入0.5万元，经市场调查知这种产品年需求量为500件，产品销售数量为t件时，销售所得的收入为万元.

    （1）该公司这种产品的年生产量为x件，生产并销售这种产品所得到的利润关于当年产量x的函数为f（x），求f（x）；

    （2）当该公司的年产量为多少件时，当年所获得的利润最大

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间和极值；

    （2）证明：当时，函数没有零点（提示：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试，分数分布如表：

    分数区间

    甲班频率

    乙班频率

    0.1

    0.2

    0.2

    0.2

    0.3

    0.3

    0.2

    0.2

    0.2

    0.1

    （Ⅰ）若成绩120分以上（含120分）为优秀，求从乙班参加测试的90分以上（含90分）的同学中，随机任取2名同学，恰有1人为优秀的概率；

    （Ⅱ）根据以上数据完成下面的×列联表：

    优秀

    不优秀

    总计

    甲班

    乙班

    总计

    在犯错概率小于0.1的前提下，你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系？

    参考公式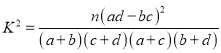：，其中

    ≥

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在区间上的奇函数，且，若时，有成立．

    （1）证明：函数在区间上是增函数；

    （2）解不等式；

    （3）若不等式对恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知等边中，分别为边的中点，为的中点，为边上一点，且，将沿折到的位置，使平面平面.

    （I）求证：平面平面；

    （II）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列结论正确的是（ ）

    ①函数关系是一种确定性关系；

    ②相关关系是一种非确定性关系；

    ③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；

    ④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法．

    A. ①② B. ①②③ C. ①②④ D. ①②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知以点为圆心的圆过原点.

    （1）设直线与圆交于点，若，求圆的方程；

    （2）在（1）的条件下，设，且分别是直线和圆上的动点，求的最大值及此时点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形是边长为2的菱形，,E,F分别为的中点，将沿折起，使得.

    （1）求证：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案