
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
分析 解法一:构造等式关系,利用基本不等式的性质即可得出.
解法二:换元法,利用三角函数的有界限求最小值.
解答 解:解法一:∵x>0,y>0,x2+y2=1
∴$\frac{1}{x}+\frac{1}{y}$>0,则有:($\frac{1}{x}+\frac{1}{y}$)2=$\frac{1}{{x}^{2}}+\frac{1}{{y}^{2}}+\frac{2}{xy}=\frac{{x}^{2}+{y}^{2}}{{x}^{2}}+\frac{{x}^{2}+{y}^{2}}{{y}^{2}}+\frac{2}{xy}$≥2+2$\sqrt{\frac{{x}^{2}}{{y}^{2}}•\frac{{y}^{2}}{{x}^{2}}}+\frac{2}{xy}$
=4+$\frac{2}{xy}$当且仅当$\frac{{x}^{2}}{{y}^{2}}=\frac{{y}^{2}}{{x}^{2}}$即x=y时取等号.
由∵1=x2+y2≥2xy,当且仅当x=y时取等号.
∴$\frac{1}{2}≥xy$
所以:$\frac{1}{x}+\frac{1}{y}$≤2$\sqrt{2}$
故选B.
解法二:换元法,
由题意:x>0,y>0,x2+y2=1
设:x=sinθ,y=cosθ($0<θ<\frac{π}{2}$)
则有:1≥2sinθ•cosθ
∴$\frac{1}{2}≥sinθ•cosθ$
$sinθ+cosθ≥2\sqrt{sinθ•cosθ}$当且仅当sinθ=cosθ时,即θ=$\frac{π}{4}$时,取等号.
那么:$\frac{1}{x}+\frac{1}{y}$=$\frac{1}{sinθ}+\frac{1}{cosθ}$=$\frac{sinθ+cosθ}{sinθ•cosθ}$≤$\frac{\sqrt{2}}{\frac{1}{2}}$=2$\sqrt{2}$.当且仅当sinθ=cosθ时,即θ=$\frac{π}{4}$时,取等号.
所以:$\frac{1}{x}+\frac{1}{y}$≤2$\sqrt{2}$
故选B.
点评 本题考查了基本不等式的性质、一元二次不等式的解法,考查了计算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
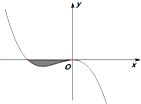 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
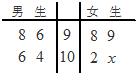 如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.
如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\overrightarrow{a}$-$\overrightarrow{b}$ | B. | -$\overrightarrow{a}$+2$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-2$\overrightarrow{b}$ | D. | 3$\overrightarrow{a}$+2$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com