
分析 (1)求出函数的导数,根据函数图象与x轴相切,求出a的值,从而求出函数的单调区间;
(2)求出g(x)的导数,通过讨论m的范围,结合函数的单调性以及f(x)>m(x-1)lnx,求出m的范围即可.
解答 解:(1)f′(x)=ex-1-a,设切点为(x0,0),
依题意,$\left\{\begin{array}{l}{f{(x}_{0})=0}\\{f′{(x}_{0})=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{{x}_{0}=1}\\{a=1}\end{array}\right.$,
所以f′(x)=ex-1-1.
当x<1时,f′(x)<0;当x>1时,f′(x)>0.
故f(x)的单调递减区间为(-∞,1),单调递增区间为(1,+∞).
(2)令g(x)=f(x)-m(x-1)lnx,x>0.
则g′(x)=ex-1-m(lnx+$\frac{x-1}{x}$)-1,
令h(x)=g′(x),则h′(x)=ex-1-m($\frac{1}{x}$+$\frac{1}{{x}^{2}}$),
(ⅰ)若m≤$\frac{1}{2}$,
因为当x>1时,ex-1>1,m($\frac{1}{x}$+$\frac{1}{{x}^{2}}$)<1,所以h′(x)>0,
所以h(x)即g′(x)在(1,+∞)上单调递增.
又因为g′(1)=0,所以当x>1时,g′(x)>0,
从而g(x)在[1,+∞)上单调递增,
而g(1)=0,所以g(x)>0,即f(x)>m(x-1)lnx成立;
(ⅱ)若m>$\frac{1}{2}$,
可得h′(x)在(0,+∞)上单调递增.
因为h′(1)=1-2m<0,h′(1+ln(2m))>0,
所以存在x1∈(1,1+ln(2m)),使得h′(x1)=0,
且当x∈(1,x1)时,h′(x)<0,所以h(x)即g′(x)在(1,x1)上单调递减,
又因为g′(1)=0,所以当x∈(1,x1)时,g′(x)<0,
从而g(x)在(1,x1)上单调递减,
而g(1)=0,所以当x∈(1,x1)时,g(x)<0,即f(x)>m(x-1)lnx不成立.
纵上所述,k的取值范围是(-∞,$\frac{1}{2}$].
点评 本小题主要考查导数的几何意义、导数及其应用、不等式等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{3}$i | B. | -1-$\sqrt{3}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,9] | B. | (0,8) | C. | [8,9] | D. | (8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
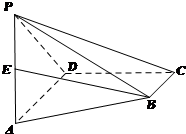 如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD,E为线段PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AD∥BC,∠ADC=90°,AD=2BC,PA⊥平面ABCD,E为线段PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 6 | 8 | 10 | 12 |
| y | 5 | m | 8 | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com