
| A. | (8,9] | B. | (0,8) | C. | [8,9] | D. | (8,+∞) |
分析 令x=y=3,利用f(3)=1即可求得f(9)=2,由f(x)+f(x-8)≤2得f[x(x-8)]≤f(9),再由单调性得到不等式组,解之即可.
解答 解:∵f(3)=1,
∴f(9)=f(3×3)=f(3)+f(3)=2;
∵函数f(x)是定义在(0,+∞)上的增函数,
f(xy)=f(x)+f(y),f(9)=2,
∴f(x)+f(x-8)≤2?f[x(x-8)]≤f(9),
∴$\left\{\begin{array}{l}{x>0}\\{x-8>0}\\{x(x-8)≤9}\end{array}\right.$,
解得:8<x≤9.
∴原不等式的解集为:(8,9].
故选:A
点评 本题考查抽象函数及其应用,着重考查赋值法与函数单调性的应用,考查解不等式组的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
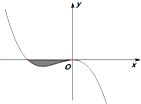 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
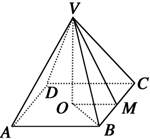 已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.
已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
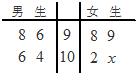 如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.
如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com