
分析 (1)求出一至四等奖的概率,即可写出分别对应的类别;
(2)若经营者不打算在这个游戏的经营中亏本,求出分布列得到期望,即可求a的最大值;
(3)若a=50,当顾客摸出的第一个球是红球,求出他领取的奖金的期望即可.
解答 解:(Ⅰ)$P(A)=\frac{C_1^1•C_3^2}{{C_{10}^3}}=\frac{3}{{C_{10}^3}}$;
$P(B)=\frac{C_3^3}{{C_{10}^3}}=\frac{1}{{C_{10}^3}}$;
$P(C)=\frac{C_6^1(C_1^1C_3^1+C_3^2)}{{C_{10}^3}}=\frac{36}{{C_{10}^3}}$;
$P(D)=\frac{C_6^2(C_1^1+C_3^1)}{{C_{10}^3}}=\frac{60}{{C_{10}^3}}$;
$P(E)=\frac{C_6^3}{{C_{10}^3}}=\frac{20}{{C_{10}^3}}$;
∵P(B)<P(A)<P(E)<P(C)<P(D),
∴中一至四等奖分别对应的类别是B,A,E,C.(4分)
(Ⅱ)设顾客进行一次游戏经营者可盈利X元,则
| X | -(a-2) | -8 | -3 | 1 | 2 |
| P | $\frac{1}{{C_{10}^3}}$ | $\frac{3}{{C_{10}^3}}$ | $\frac{20}{{C_{10}^3}}$ | $\frac{36}{{C_{10}^3}}$ | $\frac{60}{{C_{10}^3}}$ |
点评 本题考查离散型随机变量的分布列以及期望的求法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{1}{n}$ | B. | ${a_n}=\frac{1}{n+1}$ | C. | an=n | D. | ${a_n}=\frac{1}{2n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,9] | B. | (0,8) | C. | [8,9] | D. | (8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
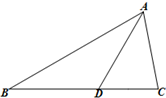 如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.
如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com