
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{12}$ |
分析 根据直线的方向向量,求得直线PQ的斜率,求得直线PQ的方程,求得与x=-2的交点坐标,求得反射直线QF1的方程,求得F1坐标,求得c的值,根据$\frac{{a}^{2}}{c}$=3,求得a的值,由椭圆的离心率公式即可求得e.
解答 解:如图,过点P(-3,1)的方向 $\overrightarrow a$=(2,-5)
∴直线PQ的斜率为:kPQ=-$\frac{5}{2}$,
根据直线方程的点斜式得:lPQ的方程为y-1=-$\frac{5}{2}$(x+3),
与y=-2的交点为 (-$\frac{9}{5}$,-2)光线经过直线y=-2反射后所在的直线方程为y+2=$\frac{5}{2}$(x+$\frac{9}{5}$),与x轴的交点(-1,0)即为椭圆的左焦点
得:c=1,$\frac{{a}^{2}}{c}$=3,则a=$\sqrt{3}$,
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,
故答案选:A.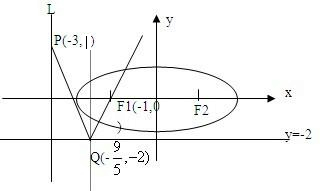
点评 本题主要考查了椭圆的简单性质、考查直线方程的求法,利用对称性求解直线方程,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,-1,0,3} | B. | {-3,-1,3} | C. | {-3,-1,1,3} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}π{R^2}$ | B. | $\frac{1}{2}π{R^2}$ | C. | πR2 | D. | 2πR2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
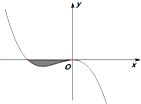 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围成区域(图中阴影部分)的面积为$\frac{1}{12}$,若函数f(x)在$({\frac{-1-k}{2},\frac{-1+k}{2}})$上单调增,求k的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com