Question

13．已知圆锥的底面半径为R，高为2R，在它的所有内接圆柱中，侧面积的最大值是（　　）

• A． $\frac{1}{4}π{R^2}$
• B． $\frac{1}{2}π{R^2}$
• C． πR²
• D． 2πR²

Answer 1

分析 设内接圆柱的底面半径为r，高为h，侧面积S=2πr•h；利用相似三角形，求出圆柱半径r与高h的关系，利用基本不等式即可求最大值．

解答 解：（如图）由题意可知：OS=2R，OC=R，内接圆柱的底面半径为OA=r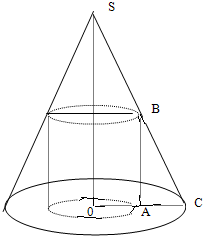，AB=h．
∵△SOC∽△ABC
∴$\frac{OS}{OC}=\frac{AB}{AC}$
AC=R-r．
则有：$\frac{2R}{R}=\frac{h}{R-r}$
∴h=2R-2r
那么：圆柱侧面积S=2πr•h=π•2r•（2R-2r）$≤π（\frac{2r+2R-2r}{2}）^{2}$=πR²
故选C

点评 本题考查了圆锥内接圆柱的问题，找到圆柱与圆锥的尺寸关系是解决本题的关键．同时考查了基本不等式的运用．属于中档题．