
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 建立空间直角坐标系,设MN是直线A1C1与AB1的公垂线,求出向量的坐标,即可得出结论.
解答 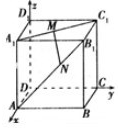 解:如图,建立空间直角坐标系,A(1,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),
解:如图,建立空间直角坐标系,A(1,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),
∴$\overrightarrow{A{B}_{1}}$=(0,1,1),$\overrightarrow{{A}_{1}{C}_{1}}$=(-1,1,0),$\overrightarrow{{A}_{1}A}$=(0,0,-1).
设MN是直线A1C1与AB1的公垂线,且$\overrightarrow{AN}$=λ$\overrightarrow{A{B}_{1}}$=(1,λ,λ),$\overrightarrow{{A}_{1}M}$=μ$\overrightarrow{{A}_{1}{C}_{1}}$=(-μ,μ,0),
则$\overrightarrow{MN}$=-(-μ,μ,0)+(0,0,-1)+(0,λ,λ)=(μ,λ-μ,λ-1).
从而有$\left\{\begin{array}{l}{λ-2μ=0}\\{2λ-μ=1}\end{array}\right.$,∴λ=$\frac{2}{3}$,μ=$\frac{1}{3}$.
∴$\overrightarrow{MN}$=($\frac{1}{3},\frac{1}{3},-\frac{1}{3}$)
∴$|\overrightarrow{MN}|$=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查空间距离的计算,考查向量知识的运用,正确运用向量是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 6 | 7 | 9 | 12 | 22 | 20 | 15 | 14 |
| 乙 | 8 | 9 | 11 | 21 | 22 | 19 | 15 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25° | B. | 65° | C. | 115° | D. | 155° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
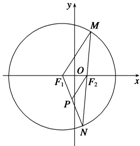 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )| A. | $\frac{4}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}π{R^2}$ | B. | $\frac{1}{2}π{R^2}$ | C. | πR2 | D. | 2πR2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com