
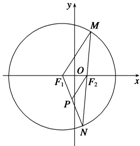
 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )| A. | $\frac{4}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$ |
分析 由题意可得$\frac{P{F}_{2}}{M{F}_{1}}=\frac{PN}{{F}_{1}N}$,得$\frac{P{F}_{2}}{4}=\frac{4-P{F}_{1}}{4}$,即PF1+PF2=4>F1F2=2,由此说明点P的轨迹为椭圆,求出椭圆方程,在设lAB为:y=k(x-1),联立直线方程和椭圆方程,化为关于x的一元二次方程,然后利用根与系数的关系求得答案.
解答 解:∵F2P∥MF1,∴$\frac{P{F}_{2}}{M{F}_{1}}=\frac{PN}{{F}_{1}N}$,得$\frac{P{F}_{2}}{4}=\frac{4-P{F}_{1}}{4}$,则PF1+PF2=4>F1F2=2,
∴点P的轨迹是以F1,F2为焦点,长轴长2a=4的椭圆,其轨迹方程为$\frac{x2}{4}$+$\frac{y2}{3}$=1.
设lAB为:y=k(x-1),联立$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,可得:(3+4k2)x2-8k2x+4k2-12=0,
不妨设A(x1,y1),B(x2,y2) (x2<1<x1),
则${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
∴$\frac{1}{|{F}_{2}A|}+\frac{1}{|{F}_{2}B|}=\frac{1}{\sqrt{1+{k}^{2}}|{x}_{1}-1|}+\frac{1}{\sqrt{1+{k}^{2}}|{x}_{2}-1|}$
=$\frac{1}{\sqrt{1+{k}^{2}}}(\frac{1}{{x}_{1}-1}+\frac{1}{1-{x}_{2}})=\frac{1}{\sqrt{1+{k}^{2}}}•\frac{{x}_{1}-{x}_{2}}{{x}_{1}+{x}_{2}-{x}_{1}{x}_{2}-1}$
=$\frac{1}{\sqrt{1+{k}^{2}}}•\frac{\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}}{{x}_{1}+{x}_{2}-{x}_{1}{x}_{2}-1}$=$\frac{1}{\sqrt{1+{k}^{2}}}•\frac{\sqrt{(\frac{8{k}^{2}}{3+4{k}^{2}})^{2}-4•\frac{4{k}^{2}-12}{3+4{k}^{2}}}}{\frac{8{k}^{2}}{3+4{k}^{2}}-\frac{4{k}^{2}-12}{3+4{k}^{2}}-1}$=$\frac{1}{\sqrt{1+{k}^{2}}}•\frac{\frac{12\sqrt{1+{k}^{2}}}{3+4{k}^{2}}}{\frac{9}{3+4{k}^{2}}}$
=$\frac{12}{9}$=$\frac{4}{3}$.综上可知,变化直线l,则$\frac{1}{|F2A|}$+$\frac{1}{|F2B|}$为定值$\frac{4}{3}$.
故选:A.
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,训练了直线与椭圆位置关系的应用,考查计算能力,是中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{-{x^3}}$与$g(x)=x\sqrt{-x}$ | B. | $f(x)=\frac{(2x-1)(x-2)}{x-2}$与g(x)=2x-1 | ||
| C. | f(x)=x0与g(x)=1 | D. | f(x)=x2-2x-1与g(t)=t2-2t-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{1}{n}$ | B. | ${a_n}=\frac{1}{n+1}$ | C. | an=n | D. | ${a_n}=\frac{1}{2n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com