
分析 根据题意,做出函数在一个周期上的图象,观察函数的图象,分别求解函数的周期,最值及取得最值的条件分别进行验证即可.
解答 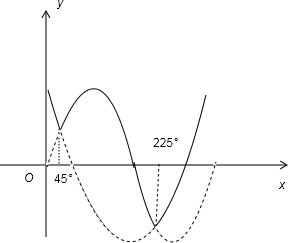 解:做出正弦函数y=sinx与y=cosx在一个周期上的图象如下图,取函数的最大值
解:做出正弦函数y=sinx与y=cosx在一个周期上的图象如下图,取函数的最大值
观察函数的图象可得函数的最小值为-$\frac{\sqrt{2}}{2}$,故①错误
观察图象可知函数以2π为周期的周期函数,故②正确;
当且仅当x=2kπ(k∈Z)时,f(x)取最大值;所以③错误;
当且仅当2kπ-$\frac{π}{2}$<x<(2k+1)π(k∈Z)时,f(x)>0,故④正确;
由图象可知相邻的最低点的距离为一个周期即2π,故⑤正确
故答案为:②④⑤.
点评 本题主要考查了正弦函数与余弦函数的图象,三角函数的性质的应用,考查了识别图象的能力及由图象研究函数的性质.解题的关键是要由题中的定义找出函数所对应的图象,结合图象求解函数的性质,体会数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
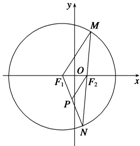 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连接MF2并延长交圆F1于点N,连接F1N,过F2作F2P∥MF1交NF1于P,如图所示.若从F2点引一条直线l交轨迹P于A,B两点,变化直线l (l的斜率一直存在),则$\frac{1}{{|F}_{2}A|}$+$\frac{1}{|{F}_{2}B|}$的值( )| A. | $\frac{4}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
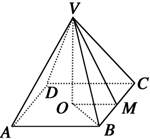 已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.
已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com