练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．平面上有n条直线，它们任何两条不平行，任何三条不共点，设k条这样的直线把平面分成f（k）个区域，且已知f（2）=4，f（3）=7，f（4）=11，则f（5）=16，k+1条直线把平面分成的区域数f（k+1）=f（k）+k+1．

    分析 1条直线把平面分成2个区域，2条直线马平面分成2+2个区域，3条把平面分成2+2+3个区域，4条直线把平面分成2+2+3+4个区域，由此可知若n条直线把平面分成f（k）个区域，则f（k+1）-f（k）=k+1．

    解答 解：1条直线把平面分成2个区域，
    2条直线马平面分成2+2个区域，
    3条把平面分成2+2+3个区域，
    4条直线把平面分成2+2+3+4个区域，
    5条直线把平面分成2+2+3+4+5=16个区域，
    由此可知若n条直线把平面分成f（k）个区域，则f（k+1）-f（k）=k+1．
    故答案为：16，k+1．

    点评 本题主要考查了归纳推理，以及数列递推式，属于中档题．所谓归纳推理，就是从个别性知识推出一般性结论的推理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知圆锥的底面半径为R，高为2R，在它的所有内接圆柱中，侧面积的最大值是（　　）
    A．$\frac{1}{4}π{R^2}$B．$\frac{1}{2}π{R^2}$C．πR2D．2πR2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某人经营一个抽奖游戏，顾客花费2元钱可购买一次游戏机会，每次游戏中，顾客从装有1个黑球，3个红球，6个白球的不透明袋子中依次不放回地摸出3个球（除颜色外其他都相同），根据摸出的球的颜色情况进行兑奖，顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金a元、10元、5元、1元，若经营者将顾客摸出的3个球的颜色情况分成以下类别：A：1个黑球2个红球；B：3个红球；C：恰有1个白球；D：恰有2个白球；E：3个白球．且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次．
    （1）请写出一至四等奖分别对应的类别（写出字母即可）；
    （2）若经营者不打算在这个游戏的经营中亏本，求a的最大值；
    （3）若a=50，当顾客摸出的第一个球是红球时，求他领取的奖金的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

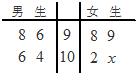    11．如图所示，高二月考考试后，将高二（3）班男生、女生各四名同学的数学成绩（单位：分）用茎叶图表示．女生某个数据的个位数模糊，记为x，已知男生、女生的平均成绩相同．
    （Ⅰ）求x的值，并判断男生与女生哪组学生成绩更稳定；
    （Ⅱ）在男生、女生中各抽取1名同学，求这2名同学的得分之和低于200分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．函数f（x）=Asin（ωx+φ）+1（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）在x=$\frac{π}{3}$处取最大值为3，其图象相邻两条对称轴之间的距离为$\frac{π}{2}$，
    （1）求函数f（x）的解析式；
    （2）设x∈[0，$\frac{π}{2}$]，f（x）求的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知实数a，函数f（x）=ex-1-ax的图象与x轴相切．
    （1）求实数a的值及函数f（x）的单调区间；
    （2）当x＞1时，f（x）＞m（x-1）lnx，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．为研究“在n次独立重复试验中，事件A恰好发生k次的概率的和”这个课题，我们可以分三步进行研究：（I）取特殊事件进行研究；（Ⅱ）观察分析上述结果得到研究结论；（Ⅲ）试证明你得到的结论．现在，请你完成：
    （1）抛掷硬币4次，设P0，P1，P2，P3，P4分别表示正面向上次数为0次，1次，2次，3次，4次的概率，求P0，P1，P2，P3，P4（用分数表示），并求P0+P1+P2+P3+P4；（2）抛掷一颗骰子三次，设P0，P1，P2，P3分别表示向上一面点数是3恰好出现0次，1次，2次，3次的概率，求P0，P1，P2，P3（用分数表示），并求P0+P1+P2+P3；
    （3）由（1）、（2）写出结论，并对得到的结论给予解释或给予证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求满足下列条件的实数x的取值范围：
    （1）3x＜9；
    （2）2x＞$\frac{1}{8}$；
    （3）（$\frac{1}{3}$）x＞$\root{3}{9}$；
    （4）3x＞7x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．从甲地到乙地一天有汽车5班，火车6列，轮船2轮，某人从甲地到乙地，共有不同的走法数为（　　）
    A．60种B．40种C．22种D．13种

    查看答案和解析>>

    同步练习册答案