
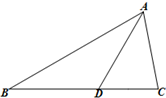
 如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.
如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.分析 (Ⅰ)解法一:由题意可知,△ABD,△ACD的两边及夹角,利用任意三角形的面积公式,求ABD的面积和ACD的面积,那么S△ABD+S△ACD=S△ABC.
解法二:过点A作BC的垂线,构造直角三角形,利用直角三角形的性质S△ABC=$\frac{1}{2}$底乘高求解.
(Ⅱ)解法一:当AD=2,BD=4时,∠ADB=180°-∠ADC=120°;在△ADB中,由余弦定理求出AB;在△ADB中,再利用正弦定理求sinB的值.
解法二:当AD=2,BD=4时,过点A作AE⊥BC于点E,∵∠ADC=60°,求出AE,DE
又因为BD=4,所以BE=BD+DE.利用直角三角形的性质,求AB,那么sinB=$\frac{AE}{AB}$即可得到答案.
解答 解:(Ⅰ)解法一:
当AD=BD=3时,△ABD的面积${S_{△ABD}}=\frac{1}{2}•AD•BD•sin∠ADB=\frac{1}{2}•3•3•\frac{{\sqrt{3}}}{2}=\frac{{9\sqrt{3}}}{4}$
ACD的面积${S_{△ACD}}=\frac{1}{2}•AD•CD•sin∠ADC=\frac{1}{2}•3•2•\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$
△ABC的面积${S_{△ABC}}={S_{△ABD}}+{S_{△ACD}}=\frac{{9\sqrt{3}}}{4}+\frac{{3\sqrt{3}}}{2}=\frac{{15\sqrt{3}}}{4}$.
解法二:
当AD=BD=3时,过点A作AE⊥BC于点E,如上图所示.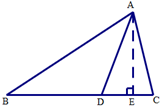 因为∠ADC=60°,所以$AE=ADsin∠ADE=3×sin{60^0}=\frac{{3\sqrt{3}}}{2}$
因为∠ADC=60°,所以$AE=ADsin∠ADE=3×sin{60^0}=\frac{{3\sqrt{3}}}{2}$
又因为CD=2,所以BC=BD+CD=5.
所以:△ABC的面积${S_{△ABC}}=\frac{1}{2}BC•AE=\frac{{15\sqrt{3}}}{4}$.(Ⅱ)解法一:
当AD=2,BD=4时,∠ADB=180°-∠ADC=120°;
在△ADB中,由余弦定理AB2=AD2+BD2-2AD•BDcos∠ADB,即:${2^2}+{4^2}-2×2×4×({-\frac{1}{2}})=28$
解得:$AB=2\sqrt{7}$.
在△ADB中,由正弦定理得$\frac{AB}{sin∠ADB}=\frac{AD}{sin∠B}$,即$\frac{{2\sqrt{7}}}{{\frac{{\sqrt{3}}}{2}}}=\frac{2}{sin∠B}$,
解得:$sin∠B=\frac{{\frac{{\sqrt{3}}}{2}}}{{\sqrt{7}}}=\frac{{\sqrt{21}}}{14}$.
解法二:
当AD=2,BD=4时,过点A作AE⊥BC于点E,如图所示,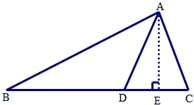
∵∠ADC=60°,
∴$AE=ADsin∠ADE=2×sin{60^0}=\sqrt{3}$
DE=ADcos∠ADE=2×cos60°=1,
又因为BD=4,所以BE=BD+DE=5.
所以:$AB=\sqrt{A{E^2}+B{E^2}}=2\sqrt{7}$
故$sinB=\frac{AE}{AB}=\frac{{\sqrt{3}}}{{2\sqrt{7}}}=\frac{{\sqrt{21}}}{14}$.
点评 本题主要考查了三角形的正弦定理和余弦定理的运用,考查运算能力,本题利用了初中的直角三角形的性质,作成勾股定理求解.高中的正余弦定理有时候解题计算麻烦,任意三角形的面积公式在知道两条边及其夹角时,计算比较简单.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com