
分析 ①根据诱导公式化简函数y=cos($\frac{2017π}{2}$+x),判断函数的奇偶性;
②求出正切函数的对称中心,即可判断命题正确;
③举反例说明命题错误;
④利用正弦、余弦和正切函数的图象与性质即可判断命题正确.
解答 解:对于①,y=cos($\frac{2017π}{2}$+x)=-sinx,是定义域R上的奇函数,原命题错误;
对于②,令x+$\frac{π}{4}$=kπ或x+$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈Z,
解得x=kπ-$\frac{π}{4}$或x=kπ+$\frac{π}{4}$,k∈Z,
当k=0时,x=±$\frac{π}{4}$,
∴函数y=tan(x+$\frac{π}{4}$)图象的一个对称中心是($\frac{π}{4}$,0),命题正确;
对于③,α=45°,β=390°时,α、β是第一象限角,且α<β,但tanα>tanβ,原命题错误;
对于④,$\frac{π}{4}$<1<$\frac{π}{2}$,
∴cos1<sin1<tan1,命题正确.
综上,以上正确的命题序号是②④.
故答案为:②④.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了命题真假的判断问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
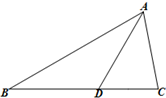 如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.
如图,在△ABC中,点D在BC边上,∠ADC=60°,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com