
分析 由条件可知$[{\begin{array}{l}1&a\\{-1}&4\end{array}}][\begin{array}{l}2\\ 1\end{array}]=λ[\begin{array}{l}2\\ 1\end{array}]$,可得方程组,即可求实数a,λ的值及A2.
解答 解:由条件可知$[{\begin{array}{l}1&a\\{-1}&4\end{array}}][\begin{array}{l}2\\ 1\end{array}]=λ[\begin{array}{l}2\\ 1\end{array}]$,
∴$\left\{\begin{array}{l}2+a=2λ\\-2+4=λ\end{array}\right.$,解得a=λ=2. …(5分)
因此$A=[{\begin{array}{l}1&2\\{-1}&4\end{array}}]$,所以${A^2}=[{\begin{array}{l}1&2\\{-1}&4\end{array}}][{\begin{array}{l}1&2\\{-1}&4\end{array}}]=[{\begin{array}{l}{-1}&{10}\\{-5}&{14}\end{array}}]$. …(10分)
点评 本题考查待定系数法求矩阵,考查特征值与特征向量,理解特征值、特征向量的定义是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}})∪({0,4})$ | B. | $({-∞,-4})∪({\frac{1}{2},1})$ | C. | $({-\frac{1}{2},0})∪({4,+∞})$ | D. | $({-∞,0})∪({\frac{1}{2},4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
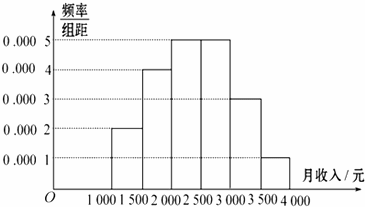
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com