
分析 (1)由题意知Sn+Sn-2=2Sn-1+n(n≥3),可得Sn-Sn-1+Sn-2-Sn-1=n(n≥3),即可得出.
(2)由an=an-1+n,利用“累加求和”方法、等差数列的求和公式即可得出.
(3)由${b_n}=|{\frac{{4{a_n}}}{n}-10}|=|{2n-8}|,n∈{N^*}$,可得${b_n}=\left\{{\begin{array}{l}{8-2n,n≤3}\\{2n-8,n≥4}\end{array}}\right.$,利用等差数列的求和公式即可得出.
解答 (1)证明:由题意知Sn+Sn-2=2Sn-1+n(n≥3),∴Sn-Sn-1+Sn-2-Sn-1=n(n≥3),
∴an-an-1=n,即an=an-1+n.
(2)解:由an=an-1+n,
∴${a_n}=({{a_n}-{a_{n-1}}})+({{a_{n-1}}-{a_{n-1}}})+…+({{a_3}-{a_2}})+{a_2}=\frac{{{n^2}+n}}{2}$.
检验知n=1,2时,结论也成立,故${a_n}=\frac{{{n^2}+n}}{2}$.
(3)解:由${b_n}=|{\frac{{4{a_n}}}{n}-10}|=|{2n-8}|,n∈{N^*}$,
∴${b_n}=\left\{{\begin{array}{l}{8-2n,n≤3}\\{2n-8,n≥4}\end{array}}\right.$,
n≤3时,Tn=6+…+(8-2n)=$\frac{n(6+8-2n)}{2}$=(7-n)n.
n≥4时,Tn=12+0+2+…+(2n-8)
=12+$\frac{(n-3)(0+2n-8)}{2}$=n2-7n+24.
故${T_n}=\left\{{\begin{array}{l}{({7-n})n,n≤3}\\{{n^2}-7n+24,n≥4}\end{array}}\right.$.
点评 本题考查了“累加求和”方法、等差数列的通项公式与求和公式、绝对值数列求和问题,考查了分类讨论、推理能力与计算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | {-3,-1,0,3} | B. | {-3,-1,3} | C. | {-3,-1,1,3} | D. | {-3,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
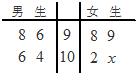 如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.
如图所示,高二月考考试后,将高二(3)班男生、女生各四名同学的数学成绩(单位:分)用茎叶图表示.女生某个数据的个位数模糊,记为x,已知男生、女生的平均成绩相同.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com