
| A. | -$\frac{8}{5}$ | B. | -$\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
分析 根据已知中函数的周期性,结合f(-$\frac{5}{2}$)=f($\frac{9}{2}$),可得m值,进而得到f(5m)的值.
解答 解:∵f(x)满足f(x+1)=f(x-1),
∴f(x+1+1)=f(x+1-1),
即f(x+2)=f(x),
∴f(x)是定义在R上且周期为2的函数,
在区间[-1,1)上,f(x)=$\left\{\begin{array}{l}x-m,-1≤x<0\\|{x-\frac{2}{5}}|,0≤x<1\end{array}$,其中m∈R,
∴f(-$\frac{5}{2}$)=f(-$\frac{1}{2}$)=-$\frac{1}{2}$-m,f($\frac{9}{2}$)=|$\frac{2}{5}$-$\frac{1}{2}$|=$\frac{1}{10}$,
∴m=-$\frac{3}{5}$
∴f(5m)=f(3)=f(-1)=-1+$\frac{3}{5}$=$\frac{2}{5}$,
故选:B
点评 本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出m值,是解答的关键.


科目:高中数学 来源: 题型:解答题
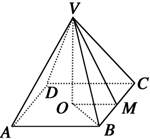 已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.
已知四棱锥V-ABCD的底面是面积为16的正方形ABCD,侧面是全等的等腰三角形,一条侧棱长为2$\sqrt{11}$,计算它的高和侧面三角形底边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,-1) | B. | (-1,1) | C. | (1,2) | D. | (-4,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com