
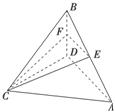
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E、F分别是AB、BD的中点,求证:
(1)直线EF∥平面ACD;
(2)平面EFC⊥平面BCD.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
下列结论正确的是( )
A.各个面都是三角形的几何体是三棱锥
B.以正方形的一条对角线为轴旋转一周围成的几何体叫圆锥
C.棱锥的侧棱长与底面多边形的边长都相等,则此棱锥可能是正六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l∥平面α,P∈α,那么过点P且平行于直线l的直线( )
A.只有一条,不在平面α内
B.有无数条,不一定在平面α内
C.只有一条,且在平面α内
D.有无数条,一定在平面α内
查看答案和解析>>
科目:高中数学 来源: 题型:
已知α,β是两个不同的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
A.若m∥α,α∩β=n,则m∥n
B.若m⊥α,m⊥n,则n∥α
C.若m⊥α,n⊥β,α⊥β,则m⊥n
D.若α⊥β,α∩β=n,m⊥n,则m⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
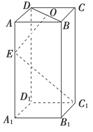
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.
(1)证明:BD⊥EC1;
(2)如果AB=2,AE=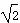 ,OE⊥EC1,求AA1的长
,OE⊥EC1,求AA1的长 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点E、F分别在正方体ABCDA1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某个体服装店经营某种服装,一周内获纯利y(元)与该周每天销售这种服装的件数x之间的一组数据如下:
| x | 3[ | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81[ | 89 | 90 | 91 |
已知: x
x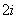 =280,
=280,
 y
y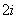 =45309,
=45309, xiyi=3487,此时r0.05=0.754.
xiyi=3487,此时r0.05=0.754.
(1)求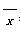 ,
,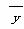 ;
;
(2)判断纯利润y与每天销售件数x之间是否线性相关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com