
【题目】设函数 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其图象上任意一点P(x0 , y0)处切线的斜率
,其图象上任意一点P(x0 , y0)处切线的斜率 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若a=2,试求f(x)在区间 ![]() 上的最大值.
上的最大值.
【答案】
(1)解:f(x)的定义域为(0,+∞),
∵f′(x)= ![]() ﹣ax+b,
﹣ax+b,
f′(1)=1﹣a+b=0,
∴b=a+1
(2)解:F(x)=lnx+ ![]() ,
,
∴F′(x)= ![]() ﹣
﹣ ![]() =
= ![]()
∴k=F′(x)= ![]() ≤
≤ ![]() 在(0,3]上恒成立,
在(0,3]上恒成立,
∴a≥(﹣ ![]() x02+x0)max,x0∈(0,3],
x02+x0)max,x0∈(0,3],
当x0=1时,﹣ ![]() x02+x0的取得最大值
x02+x0的取得最大值 ![]() ,
,
∴a≥ ![]()
(3)解:当a=2时,f(x)=lnx﹣x2+x,
∴f′(x)= ![]() ﹣2x+1=
﹣2x+1= ![]() ,
,
令f′(x)=0,解得x=1或x=﹣ ![]() (舍去),
(舍去),
当0<x<1时,f′(x)>0,此时f(x)单调递增,
当x>1时,f′(x)<0,此时f(x)单调递减,
当c+ ![]() ≤1,即0<c≤
≤1,即0<c≤ ![]() 时,f(x)区间
时,f(x)区间 ![]() 上单调递增,
上单调递增,
∴f(x)max=f(c+ ![]() )=ln(c+
)=ln(c+ ![]() )﹣(c+
)﹣(c+ ![]() )2+c+
)2+c+ ![]() =ln(c+
=ln(c+ ![]() )+
)+ ![]() ﹣c2,
﹣c2,
当 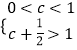 .即
.即 ![]() <c<1时,f(x)在[c,1]上单调递增,在[1,c+
<c<1时,f(x)在[c,1]上单调递增,在[1,c+ ![]() ]上单调递减,
]上单调递减,
∴f(x)max=f(1)=0,
当c≥1时,f(x)在[c,c+ ![]() ]上单调递减,
]上单调递减,
∴f(x)max=f(c)=lnc﹣c2+c,
综上所述,当0<c≤ ![]() 时,f(x)max=ln(c+
时,f(x)max=ln(c+ ![]() )+
)+ ![]() ﹣c2,
﹣c2,
当 ![]() <c<1时,f(x)max=0,
<c<1时,f(x)max=0,
当c≥1时,f(x)max=lnc﹣c2+c
【解析】(1)先求导,再代值计算即可得到b=a+1;(2)根据导数的几何意义求出直线的斜率,再根据二次函数的性质求出a的范围;(3)求导,分类讨论,根据导数和函数的最大值得关系即可求出.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】图是函数y=Asin(ωx+φ)(x∈R)在区间 ![]() 上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
上的图象,为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ![]() ,∠CDA=120°,点N在线段PB上,且PN=2.
,∠CDA=120°,点N在线段PB上,且PN=2. 
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)若函数f(x)=|2x﹣1|+|2x﹣3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)= ![]() 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数![]() ,当x∈(-3,2)时,
,当x∈(-3,2)时,![]() >0,当x∈(-
>0,当x∈(-![]() ,-3)
,-3)![]() (2,+
(2,+![]() )时,
)时,![]() <0
<0
(I)求a,b的值;
(II)若不等式![]() 的解集为R,求实数c的取值范围.
的解集为R,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知整数n≥4,集合M={1,2,3,…,n}的所有含有4个元素的子集记为A1 , A2 , A3 , …, ![]() .
.
设A1 , A2 , A3 , …, ![]() 中所有元素之和为Sn .
中所有元素之和为Sn .
(1)求S4 , S5 , S6并求出Sn;
(2)证明:S4+S5+…+Sn=10Cn+26 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com