
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 可画出图形,设A,B,C所对的边分别为a,b,c,并设AD=m,这样根据便可得到$bm=\frac{bc}{2}$,从而得到m=$\frac{c}{2}$,这样在△ABD中由余弦定理便可建立关于c的方程,可解出c=$2\sqrt{3}$,从而有m=$\sqrt{3}$,然后进行数量积的计算便可求出$\overrightarrow{AD}•\overrightarrow{AB}$的值.
解答 解:如图,设△ABC的内角A,B,C所对的边分别为a,b,c,且设AD=m;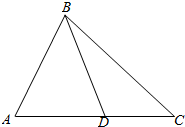
∵∠A=60°,∴由$\overrightarrow{AC}•\overrightarrow{AD}=\overrightarrow{AC}•\overrightarrow{AB}$得:$bm=\frac{bc}{2}$;
∴$m=\frac{c}{2}$;
又BD=3,∴在△ABD中由余弦定理得:
$9=\frac{{c}^{2}}{4}+{c}^{2}-\frac{{c}^{2}}{2}$;
∴$c=2\sqrt{3}$,m=$\sqrt{3}$;
∴$\overrightarrow{AD}•\overrightarrow{AB}=mc•cos60°=\sqrt{3}•2\sqrt{3}•\frac{1}{2}=3$.
故选:C.
点评 考查向量数量积的计算公式,余弦定理,以及向量夹角的概念.


科目:高中数学 来源: 题型:选择题
| A. | -2tanα | B. | 2tanα | C. | -tanα | D. | tanα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=9 | B. | (x-2)2+y2=16 | C. | (x+1)2+y2=9 | D. | (x+2)2+y2=16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
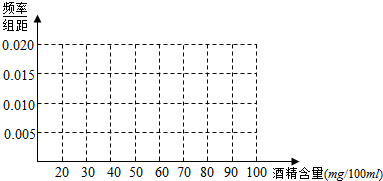
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com