
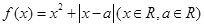 .
.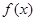 的奇偶性;
的奇偶性;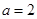 时,求
时,求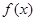 的单调区间;
的单调区间;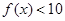 对
对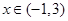 恒成立,求实数
恒成立,求实数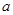 的取值范围.
的取值范围.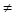 0时函数f(x)为非奇非偶函数
0时函数f(x)为非奇非偶函数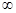 ,
, ),增区间为(
),增区间为( ,+
,+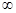 );(3)
);(3) 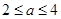
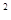 +
+
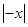 =x
=x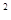 +
+ =f(x)
=f(x) 函数f(x)为偶函数3分
函数f(x)为偶函数3分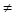 0时:
0时: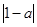 ,f(-1)=1+
,f(-1)=1+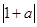
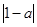 =1+
=1+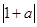 从而a=0,舍去;
从而a=0,舍去;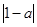 +
+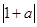 =-2从而a
=-2从而a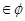
 f(1)
f(1)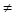 ±f(-1),
±f(-1), 函数f(x)为非奇非偶函数6分
函数f(x)为非奇非偶函数6分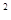 +
+ =
=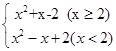
 原函数的减区间为(-
原函数的减区间为(-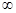 ,
, ),增区间为(
),增区间为( ,+
,+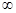 );10分
);10分 (-1,3)
(-1,3) f(x)<10可变为x
f(x)<10可变为x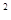 -10<a-x< 10-x
-10<a-x< 10-x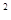
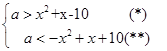
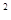 +x-10,其对称轴为
+x-10,其对称轴为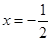
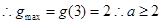 ③
③
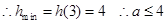 ④
④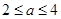 16分
16分

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源:不详 题型:解答题
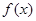 是定义在区间
是定义在区间 上的偶函数,且满足
上的偶函数,且满足
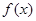 的周期;
的周期; 时,
时, .求使方程
.求使方程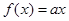 在
在 上有两个不相等实根的
上有两个不相等实根的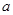 的取值集合M.
的取值集合M.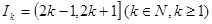 ,
, 表示使方程
表示使方程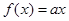 在
在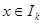 上有两个不相等实根的
上有两个不相等实根的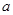 的取值集合,求集合
的取值集合,求集合 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com