
分析 (Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)对a2、a3分类取值,再结合各项均为非负整数列式求m的值;
(Ⅲ)令Sn=a1+a2+…+an,则$\frac{{{S_{n+1}}}}{n+1}<\frac{{{S_{n+1}}}}{n}=\frac{{{S_n}+{a_{n+1}}}}{n}≤\frac{{{S_n}+n}}{n}=\frac{S_n}{n}+1$.进一步推得存在正整数M>m,当n>M时,必有$\frac{{{S_{n+1}}}}{n+1}=\frac{S_n}{n}$成立.再由$\frac{{{S_{n+1}}}}{n+1}=\frac{S_n}{n}$成立证明an为常数.
解答 (Ⅰ)解:m=5时,数列{an}的前五项分别为:5,1,0,2,2.
(Ⅱ)解:∵0≤an≤n-1,∴0≤a2≤1,0≤a3≤2,
又数列{an}的前3项互不相等,
(1)当a2=0时,
若a3=1,则a3=a4=a5=…=1,
且对n≥3,$\frac{m+0+(n-2)}{n}=\frac{m-2}{n}+1$都为整数,∴m=2;
若a3=2,则a3=a4=a5=…=2,
且对n≥3,$\frac{m+0+2(n-2)}{n}=\frac{m-4}{n}+2$都为整数,∴m=4;
(2)当a2=1时,
若a3=0,则a3=a4=a5=…=0,
且对n≥3,$\frac{m+1+0•(n-2)}{n}=\frac{m+1}{n}$都为整数,∴m=-1,不符合题意;
若a3=2,则a3=a4=a5=…=2,
且对n≥3,$\frac{m+1+2(n-2)}{n}=\frac{m-3}{n}+2$都为整数,∴m=3;
综上,m的值为2,3,4.
(Ⅲ)证明:对于n≥1,令Sn=a1+a2+…+an,
则$\frac{{{S_{n+1}}}}{n+1}<\frac{{{S_{n+1}}}}{n}=\frac{{{S_n}+{a_{n+1}}}}{n}≤\frac{{{S_n}+n}}{n}=\frac{S_n}{n}+1$.
又对每一个n,$\frac{S_n}{n}$都为正整数,∴$\frac{{{S_{n+1}}}}{n+1}$$≤\frac{S_n}{n}≤…≤\frac{S_1}{1}=m$,其中“<”至多出现m-1个.
故存在正整数M>m,当n>M时,必有$\frac{{{S_{n+1}}}}{n+1}=\frac{S_n}{n}$成立.
当$\frac{{{S_{n+1}}}}{n+1}=\frac{S_n}{n}$时,则${a_{n+1}}={S_{n+1}}-{S_n}=\frac{{(n+1){S_n}}}{n}-{S_n}=\frac{S_n}{n}$.
从而$\frac{{{S_{n+2}}}}{n+2}=\frac{{{a_{n+2}}+{a_{n+1}}+{S_n}}}{n+2}=\frac{{{a_{n+2}}+(n+1){a_{n+1}}}}{n+2}={a_{n+1}}+\frac{{{a_{n+2}}-{a_{n+1}}}}{n+2}$.
由题设知$\frac{{|{a_{n+2}}-{a_{n+1}}|}}{n+2}≤\frac{n+1}{n+2}<1$,又$\frac{{{S_{n+2}}}}{n+2}$及an+1均为整数,
∴$\frac{{{S_{n+2}}}}{n+2}$=an+1=$\frac{S_n}{n}=\frac{{{S_{n+1}}}}{n+1}$,故$\frac{S_n}{n}=\frac{{{S_{n+1}}}}{n+1}=\frac{{{S_{n+2}}}}{n+2}=…$=常数.
从而${a_{n+1}}={S_{n+1}}-{S_n}=\frac{{(n+1){S_n}}}{n}-{S_n}=\frac{S_n}{n}$=常数.
故存在正整数M,使得n≥M时,an为常数.
点评 本题考查数列递推式,考查数列的前n项和,考查逻辑思维能力与推理运算能力,体现了分类讨论的数学思想方法,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
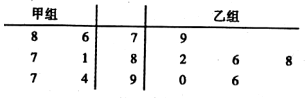 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
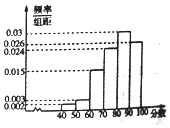 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| A | B | 合计 | |
| 认可 | |||
| 不认可 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com