
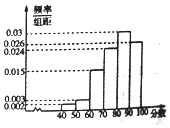
 2017��3��14�գ���ofo�������������������ߺ���ofo���������ֱ����г�����С�Ƴ�����ȫ���һ������������ƽ̨����������������������ģʽ����ز������Ը���Ŀ���п��ˣ����˵�Ӳ��ָ���ǣ�����Ը���Ŀ������ָ��������0.8���������Ŀ��������ģ��ò���Ϊ���˽�����Ը���Ŀ������̶ȣ����������ʹ�ù���������100������������100������Ը���Ŀ����̶ȵ����֣�����������Ƶ�ʷֲ�ֱ��ͼ��
2017��3��14�գ���ofo�������������������ߺ���ofo���������ֱ����г�����С�Ƴ�����ȫ���һ������������ƽ̨����������������������ģʽ����ز������Ը���Ŀ���п��ˣ����˵�Ӳ��ָ���ǣ�����Ը���Ŀ������ָ��������0.8���������Ŀ��������ģ��ò���Ϊ���˽�����Ը���Ŀ������̶ȣ����������ʹ�ù���������100������������100������Ը���Ŀ����̶ȵ����֣�����������Ƶ�ʷֲ�ֱ��ͼ������ ��I�������оٷ�ȷ�������¼������������2������ǡ�ö���[50��60���ĸ��ʣ�
��II��������������ָ�����ɵý��ۣ�
��� �⣺��I��������ã�������[40��50����[50��60����Ƶ�ʷֱ�Ϊ0.02��0.03��
����������[40��50����[50��60��������ֱ���2����3������ΪA1��A2��B1��B2��B3
�����ֵ���6��0�֣��������������ȡ2�ˣ����п��ܵĽ������10�֣�
������{A1��A2}��{A1��B1}��{A1��B2}��{A1��B3}��{A2��B1}��{A2��B2}��{A2��B3}��{B1��B2}��{B1��B3}��{B2��B3}��
����2�����ֶ���[50��60���������֣���{B1��B2}��{B1��B3}��{B2��B3}��
������ĸ���Ϊ$\frac{3}{10}$��
��II����������Ƶ�ʷֲ�ֱ��ͼ�ɵ�����̶ȵ�ƽ���÷�Ϊ45��0.02+55��0.03+65��0.15+75��0.24+85��0.3+95��0.26=80.5��
�ɹ������������ָ��Ϊ$\frac{80.5}{100}=0.805��0.8$��
���Ը���Ŀ��ͨ�����գ�
���� ���⿼����ʵļ��㣬�����оٷ������ã�����ѧ���ļ��������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 29 | B�� | 210 | C�� | 211 | D�� | 212 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��2} | B�� | {-1��0} | C�� | {0��1} | D�� | {1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[{-\frac{1}{2}-\frac{1}{{2{e^2}}}��+��}��$ | B�� | $[{-\frac{1}{{2{e^2}}}��+��}��$ | C�� | [-2��+�ޣ� | D�� | $��{-2��-\frac{1}{2}-\frac{1}{{2{e^2}}}}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{2}{{e}^{2}}$��0�� | B�� | [-$\frac{2}{{e}^{2}}$��0����{$-\frac{1}{2}$e} | C�� | [-$\frac{e}{2}$��0�� | D�� | [-$\frac{2}{{e}^{2}}$��0] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $-\frac{1}{2}$ | C�� | $\frac{1}{3}$ | D�� | $-\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com