
分析 (1)由已知数列递推式求出首项,并得到当n≥2时,3Sn-1=4(an-1-1),与原递推式作差得:an=4an-1(n≥2).得到数列{an}是以4为首项,以4为公比的等比数列,由等比数列的通项公式得答案;
(2)由a1b1+a2b2+a3b3+…+anbn=$\frac{20}{9}$+($\frac{2n}{3}$-$\frac{5}{9}$)×2${\;}^{2n+{2}^{\;}}$,得a1b1+a2b2+a3b3+…+an-1bn-1=$\frac{20}{9}$+($\frac{2n-2}{3}$-$\frac{5}{9}$)×22n(n≥2),两式作差可得数列{bn}是等差数列,然后由等差数列的前n项和求得数列{bn}的前n项和Tn.
解答 解:(1)由3Sn=4(an-1),取n=1,得3a1=3S1=4a1-4,∴a1=4;
当n≥2时,3Sn-1=4(an-1-1),
两式作差得:an=4an-1(n≥2).
∴数列{an}是以4为首项,以4为公比的等比数列,
则${a}_{n}=4×{4}^{n-1}={4}^{n}$;
(2)由a1b1+a2b2+a3b3+…+anbn=$\frac{20}{9}$+($\frac{2n}{3}$-$\frac{5}{9}$)×2${\;}^{2n+{2}^{\;}}$,
得a1b1+a2b2+a3b3+…+an-1bn-1=$\frac{20}{9}$+($\frac{2n-2}{3}$-$\frac{5}{9}$)×22n(n≥2),
两式作差可得anbn=($\frac{2n}{3}$-$\frac{5}{9}$)×2${\;}^{2n+{2}^{\;}}$-($\frac{2n-2}{3}$-$\frac{5}{9}$)×22n=(2n-1)•22n.
∴${b}_{n}=\frac{(2n-1){2}^{2n}}{{4}^{n}}=2n-1$(n≥2).
又由${a}_{1}{b}_{1}=\frac{20}{9}+(\frac{2}{3}-\frac{5}{9})×{2}^{4}$求得b1=1,
∴bn=2n-1.
∴bn+1-bn=2n+1-2n+1=2.
则数列{bn}是以1为首项,以2为公差的等差数列,
∴数列{bn}的前n项和Tn=$n×1+\frac{n(n-1)}{2}×2={n}^{2}$.
点评 本题考查数列递推式,考查等差关系的确定,训练了等差数列前n项和的求法,是中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [3kπ-$\frac{π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | B. | [3kπ-$\frac{5π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | ||
| C. | [2kπ-$\frac{2π}{3}$,2kπ-$\frac{π}{6}$],k∈Z | D. | [2kπ-$\frac{π}{3}$,2kπ-$\frac{π}{6}$],k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
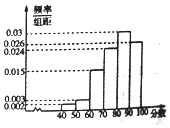 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},+∞})$ | B. | $[{\sqrt{2},+∞})$ | C. | $({1,\sqrt{2}})$ | D. | $({1,\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | (1,2) | C. | {1,2} | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com