
| A. | $({\sqrt{2},+∞})$ | B. | $[{\sqrt{2},+∞})$ | C. | $({1,\sqrt{2}})$ | D. | $({1,\sqrt{2}}]$ |
分析 设M(x0,y0),P(0,yp),Q(0,yq),通过M,P,Q三点共线,求出yp,yq,利用等比数列求出b的范围,然后求解离心率即可.
解答 解:设M(x0,y0),P(0,yp),Q(0,yq),
由M,P,Q三点共线,可知yp=$\frac{a{y}_{0}}{{x}_{0}+a}$,同理yq=$\frac{-a{y}_{0}}{{x}_{0}-a}$,
所以|OP||OQ|=$\frac{{a}^{2}{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}={b}^{2}$,从而|OM|=b,当b>a时,满足题意,所以e$>\sqrt{2}$.
故选:A.
点评 本题考查双曲线的简单性质的应用,等比数列的性质的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2}-\frac{1}{{2{e^2}}},+∞})$ | B. | $[{-\frac{1}{{2{e^2}}},+∞})$ | C. | [-2,+∞) | D. | $({-2,-\frac{1}{2}-\frac{1}{{2{e^2}}}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -6 | C. | -2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{{e}^{2}}$,0) | B. | [-$\frac{2}{{e}^{2}}$,0)∪{$-\frac{1}{2}$e} | C. | [-$\frac{e}{2}$,0) | D. | [-$\frac{2}{{e}^{2}}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
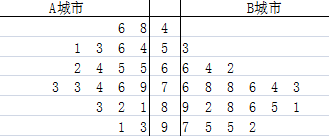
| 认可 | 不认可 | 合计 | |
| A城市 | |||
| B城市 | |||
| 合计 |
| P(Χ2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com