
| �Ͽ� | ���Ͽ� | �ϼ� | |
| A���� | |||
| B���� | |||
| �ϼ� |
| P����2��k�� | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
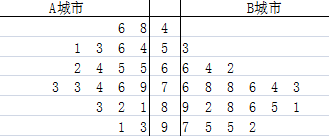
���� �����ݾ�Ҷͼ�����ɱȽ���������������ֵ�ƽ��ֵ�ͷ��
���������2�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
���������оٷ�ȷ�������¼�������������Բ�ͬ���еĸ��ʣ���
��� �⣺����A�������ֵ�ƽ��ֵС��B�������ֵ�ƽ��ֵ�� ��2�֣�
A�������ֵķ������B�������ֵķ�� ��4�֣�
����2��2������
| �Ͽ� | ���Ͽ� | �ϼ� | |
| A���� | 5 | 15 | 20 |
| B���� | 10 | 10 | 20 |
| �ϼ� | 15 | 25 | 40 |
���� ������Ҫ�������ͳ�Ƶ����֪ʶ�����龥Ҷͼ�������Լ���֪ʶ�����ã�������ʵļ��㣬�����е��⣮


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{\sqrt{2}��+��}��$ | B�� | $[{\sqrt{2}��+��}��$ | C�� | $��{1��\sqrt{2}}��$ | D�� | $��{1��\sqrt{2}}]$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -112 | B�� | -56 | C�� | 112 | D�� | 56 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��2} | B�� | ��1��2�� | C�� | {1��2} | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3025 | B�� | -3024 | C�� | 2017 | D�� | 9703 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=sin��{\frac{x}{2}+\frac{��}{6}}��$ | B�� | $y=cos��{\frac{x}{2}-\frac{��}{6}}��$ | C�� | $y=cos��{2x+\frac{��}{6}}��$ | D�� | $y=sin��{2x-\frac{��}{6}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-1��x��$\frac{1}{3}$} | B�� | {x|x��$\frac{1}{3}$} | C�� | {x|x��$\frac{1}{3}$} | D�� | {x|$\frac{1}{3}$��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
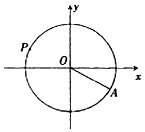 ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������
ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������| A�� | $R=6����=\frac{��}{30}����=-\frac{��}{6}$ | |
| B�� | ��t��[35��55]ʱ����P��x��ľ�������ֵΪ6 | |
| C�� | ��t��[10��25]ʱ������y=f��t�������ݼ� | |
| D�� | ��t=20ʱ��$|{PA}|=6\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{4}{5}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com