
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
分析 利用正弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
解答 解:由于y=sin($\frac{x}{2}$+$\frac{π}{6}$)的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,不满足①,故排除A.
由于y=cos($\frac{x}{2}$-$\frac{π}{6}$)的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,不满足①,故排除B.
由于y=cos(2x+$\frac{π}{6}$),在$[{-\frac{π}{6},\frac{π}{3}}]$上,2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
故y=cos(2x+$\frac{π}{6}$)在$[{-\frac{π}{6},\frac{π}{3}}]$上没有单调性,故排除C.
对于y=sin(2x-$\frac{π}{6}$)的最小正周期为$\frac{2π}{2}$=π;
当$x=\frac{π}{3}$时,函数取得最大值为1,故图象关于直线$x=\frac{π}{3}$对称;
在$[{-\frac{π}{6},\frac{π}{3}}]$上,2x-$\frac{π}{6}$∈[-$\frac{π}{2}$,$\frac{π}{2}$],故y=sin(2x-$\frac{π}{6}$)在$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数,
故D满足题中的三个条件,
故选:D.
点评 本题主要考查正弦函数的图象和性质,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{{e}^{2}}$,0) | B. | [-$\frac{2}{{e}^{2}}$,0)∪{$-\frac{1}{2}$e} | C. | [-$\frac{e}{2}$,0) | D. | [-$\frac{2}{{e}^{2}}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
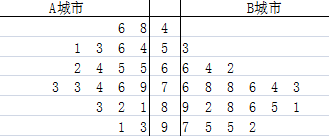
| 认可 | 不认可 | 合计 | |
| A城市 | |||
| B城市 | |||
| 合计 |
| P(Χ2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1∧p2 | B. | p1∨p2 | C. | p1∧(¬p2) | D. | (¬p1)∨p2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
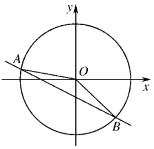 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com