
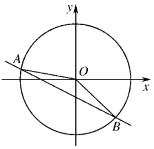
 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |
分析 分别利用勾股定理和距离公式求出O到直线AB的距离,列方程解出a即可.
解答 解:$\overrightarrow{OA}•\overrightarrow{OB}$=cos∠AOB=a,
∴AB=$\sqrt{1+1-2cos∠AOB}$=$\sqrt{2-2a}$,
∴O到直线AB的距离d=$\sqrt{1-(\frac{\sqrt{2-2a}}{2})^{2}}$,
又d=$\frac{|a|}{\sqrt{5}}$,
∴$\sqrt{1-(\frac{\sqrt{2-2a}}{2})^{2}}$=$\frac{|a|}{\sqrt{5}}$,解得a=$\frac{5-\sqrt{65}}{4}$或a=$\frac{5+\sqrt{65}}{4}$>1(舍).
故选:A.
点评 本题考查了平面向量的数量积运算,直线与圆的位置关系,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,+∞) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
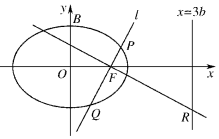 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
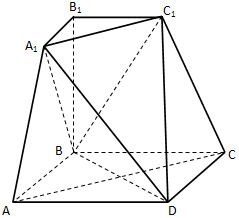 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,lnx0>x0 | B. | ?x≤0,lnx0≥x0 | C. | ?x>0,lnx0≥x0 | D. | ?x>0,lnx0<x0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com