
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 运用对数函数的单调性,可得?x∈R,y=ln(x2+1)≥ln1=0,即可判断①;
通过举x=4,x2=2x=16,即可判断②;
通过举α=60°,β=30°,计算sin(α-β),sin α-sin β即可判断③;
运用等价命题可得p是¬q成立的必要不充分条件,结合充分必要条件的定义,即可判断④.
解答 解:①?x0∈R,ln(x02+1)<0不正确,由于?x∈R,y=ln(x2+1)≥ln1=0,故①错;
②?x>2,x2>2x不正确,比如x=4,则x2=2x=16,故②错;
③?α,β∈R,sin(α-β)=sin α-sin β不正确,比如α=60°,β=30°,
sin(α-β)=sin30°=$\frac{1}{2}$,sin α-sin β=sin60°-sin30°=$\frac{\sqrt{3}-1}{2}$,显然不等,
应为?α,β∈R,sin(α-β)=sin αcosβ-cosαsin β,故③错;
④若q是¬p成立的必要不充分条件,则p是¬q成立的必要不充分条件,
则¬q是p成立的充分不必要条件,故④正确.
其中真命题的个数为1.
故选:A.
点评 本题考查命题的真假判断和应用,考查存在性命题和任意性命题的真假,注意运用反例法,考查充分必要条件的判断,注意运用等价命题的转化,考查判断能力,属于基础题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{2,\sqrt{3}+1}]$ | B. | $[{2,2\sqrt{3}+1}]$ | C. | $[{\sqrt{2},2}]$ | D. | $[{\sqrt{2},\sqrt{3}+1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
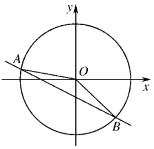 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α⊥β且m?α | B. | m∥n且n⊥β | C. | α⊥β且m∥α | D. | m⊥n且n∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com