
分析 (I)利用相互独立事件的概率公式,求出甲、乙2名学生选做同一道题的概率;
(Ⅱ)确定X的取值,求出相应的概率,即可求出X的分布列及数学期望.
解答 解:(Ⅰ)设事件A表示“甲选做第1题”,事件B表示“乙选做第1题”,
则“甲选做第2题”为$\overline{A}$,“乙选做第2题”为$\overline{B}$;
∴甲、乙2位选手选做同一道题的事件为“AB+$\overline{A}$$\overline{B}$”,且事件A、B相互独立;
∴P(AB+$\overline{A}$$\overline{B}$)=P(A)P(B)+P($\overline{A}$)P($\overline{B}$)=$\frac{1}{2}$×$\frac{1}{2}$+(1-$\frac{1}{2}$)×(1-$\frac{1}{2}$)=$\frac{1}{2}$;
(Ⅱ)随机变量ξ的可能取值为0,1,2,3,4,5,且X~B(5,$\frac{1}{2}$);
∴P(X=k)=${C}_{5}^{k}$•${(\frac{1}{2})}^{k}$•${(1-\frac{1}{2})}^{5-k}$=${C}_{5}^{k}$•${(\frac{1}{2})}^{5}$,k=0,1,2,3,4,5;
∴变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{32}$ | $\frac{5}{32}$ | $\frac{10}{32}$ | $\frac{10}{32}$ | $\frac{5}{32}$ | $\frac{1}{32}$ |
点评 本题考查了概率知识的运用问题,也考查了离散型随机变量的分布列与期望计算问题,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
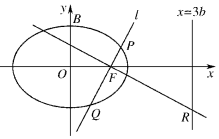 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{π}{12},\frac{π}{4}}]$ | B. | $[{\frac{π}{6},\frac{5π}{12}})$ | C. | $[{\frac{π}{6},\frac{π}{3}}]$ | D. | $({\frac{π}{6},\frac{π}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{33}}}{3}$ | C. | $\frac{{4\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{33}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
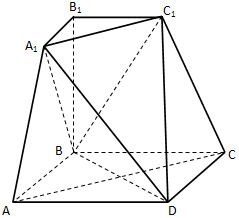 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com